16. Метод объединения простых путей с учетом эффекта поглощения (ортогонализации)

Этот метод использует представление события работоспособности системы в виде суммы несовместных (ортогональных) событий. Именно, система работоспособна, если работоспособен 1-й простой путь, либо 1-й простой путь неработоспособен, но работоспособен 2-й простой путь, либо 1-й и 2-й простые пути неработоспособны, но работоспособен 3-й простой путь и т.д. Отсюда получим:

,

где А' обозначает событие, противоположное А.

Поскольку объединяемые события здесь несовместны, их вероятности просто суммируются, поэтому

(16.1)

Число слагаемых здесь равно k, что меньше, чем при применении ранее изложенных методов. Кроме того, данный метод имеет то преимущество, что все слагаемые в (16.1) положительны. Поэтому получающиеся неполные суммы дают нижнюю оценку для вероятности Р.

Правила поглощения

События представляются в виде . Прежде чем перейти к расчету их вероятностей, эти выражения следует преобразовать, исключив все повторяющиеся переменные х_i. Для этого используются следующие правила поглощения:

(16.2)

(16.3)

(16.4)

Затем в полученную таким образом бесповторную форму вместо подставляются , а отрицание (‘) заменяется взятием дополнения до 1.

Пример

Рассмотрим опять мостик. Для него:

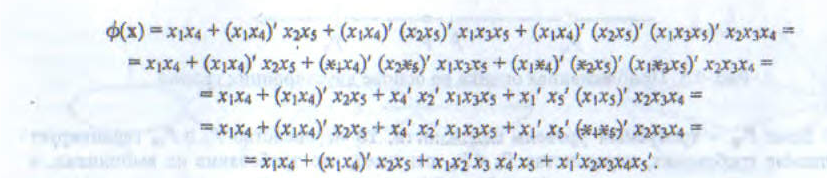
Поэтому

17. Двусторонние оценки надежности на основе простых путей и сечений.

Трудоемкость точных методов расчета надежности неприводимых систем экспоненциально растет с увеличением числа их элементов. Это делает практически невозможным точный расчет для больших систем и заставляет искать методы приближенного расчета и построения различных оценок.

Приближение для систем из элементов с одинаковой высокой надежностью

Пусть все элементы системы имеют одинаковую и высокую надежность, т.е. q_i = 1 – р_i = q << 1. Тогда, принимая в расчет только сечения с минимальным числом элементов, получим:

Р ≈ 1 - c_λq^λ , (17.1)

где λ - минимальное число элементов в сечении, c_λ – число сечений из λ элементов.

Например, для мостика (рис. 8.1) λ=2 и с_λ=2 (это сечения {1,2} и {4,5}). Поэтому

Р ≈ 1 – 2q². Для q = 0,1 получим Р ≈ 0,98 (точное значение Р = 0,97848).

Использование двусторонних оценок

Имеется целый ряд методов, позволяющих получить двусторонние оценки (границы) для вероятности работоспособности системы Р, т.е. числа и для которых . Такие оценки могут использоваться для получения приближенного значения вероятности Р и для проверки выполнения требований по надежности. Действительно, в качестве приближенного значения можно взять

При этом абсолютная погрешность не превосходит величины (рис. 9.1)

Если - требуемый уровень надежности, то неравенство гарантирует выполнение требования, неравенство означает, что требование не выполнено, и только в промежуточном случае возникает необходимость в получении более точных оценок.

Простота расчетов надежности приводимых систем позволяет использовать их для получения двусторонних оценок надежности систем неприводимых. Именно, для исходной системы S строятся такие две оценочные системы S_* и , что для них имеют место неравенства . При этом в силу приводимости оценочных систем расчет P(S_*) и P( ) для них гораздо проще, чем для исходной системы. Известны несколько способов построения оценочных систем, два из которых описаны ниже.