14. Структурно-сложные (неприводимые) системы. Расчет надежности методами полного перебора состояний и разложения по элементу. Неприводимые системы

Система, структура которой не может быть представлена в виде комбинаций последовательных и параллельных соединений, называется неприводимой. Пройтсейшей неприводимой системой является мостиковая схема. Критерием работоспособности такой системы предполагается наличие пути из работоспособных элементов между двумя полюсами.

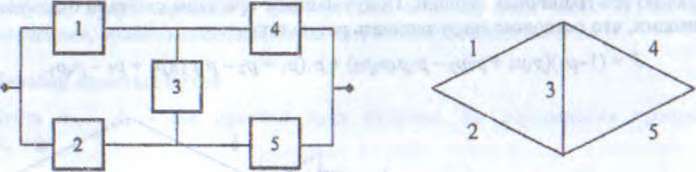
Мостиковая схема (слева – полное, справа – упрощенное изображение)

С ростом числа элементов системы n доля неприводимых систем в общем числе систем из n элементов возрастает, и при n→∞ эта доля стремится к 1.

Рассмотрим методы расчета и оценки надежности неприводимых систем.

Метод полного перебора состояний

_{Этот метод впрямую использует формулу (8.4). Расчеты удобно представить в виде таблицы, вид которой на примере мостика приведен ниже. При записи вероятностей состояний используется обозначение qi = 1 – pi}

Состояния элементов хi					Состояние системы ф(х)	Вероятность состояния р(х)
1	2	3	4	5
0	0	0	0	0	0	q1q2q3q4q5
1	0	0	0	0	0	p1q2q3q4q5
...	...	...	...	...	...	...
0	0	0	0	1	0	q1q2q3q4p5
1	1	0	0	0	0	p1p2q3q4q5
1	0	1	0	0	0	p1q2p3q4q5
1	0	0	1	0	1	p1q2q3p4q5
...	...	...	...	...	...	...
1	1	1	1	1	1	p1p2p3p4p5

Чтобы получить вероятность P, надо просуммировать вероятности всех состояний, для которых ф(x) = 1 (можно было нули и не выписывать):

P= p₁q₂q₃q₄q_5+…+ p₁p₂p₃p₄p₅.

Из-за необходимости перебора 2n состояний метод практически применим только для систем с малым числом элементов.

Метод разложения по элементу

В основе метод метода лежит применение формулы полной вероятности, в которой в качестве полной группы событий используются события {х_k = 1} и {х_k = 0} для некоторого элемента системы к. При этом расчет искомой вероятности Р = Р{ф(х) = 1} сводится к расчету условных вероятностей этого события при условиях х_k = 1 и х_k = 0:

P = p_kP {ф(x)=1 | x_k = 1}+ (1-p_k)P{ф(x)=1 | x_k = 0}.

Условие x_k=1 означает абсолютную надежность данного элемента, а x_k = 0 – его исключение из структуры системы. Элемент, по которому производится разложение, надо выбирать так, чтобы расчет указанных условных вероятностей был проще, чем полной вероятности для всей системы.

Пример

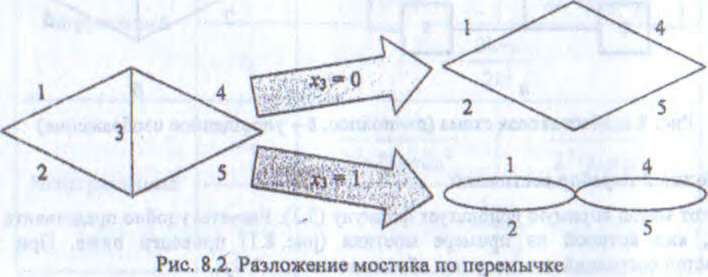
При разложении мостика по перемычке мы сначала считаем вероятность без этой перемычки (x₃=0), а потом так, как будто перемычка абсолютно надежная, (x₃=1). Это условие (x₃=1) приводит к «стягиванию» граничных вершин 3 ребра. Получившиеся при этом вероятности получаются проводимыми, т.е.:

P = (1-p₁)(p₁p₄+p₂p₅-p₁p₂p₄p₅)+ p₁(p₁+p₂-p₁p₂)(p₄+p₅-p₄p₅).

Это разложение можно применить и несколько раз, например, для такого случая:

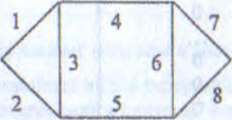
Мостик с двумя перемычками

В этом случае следует провести разложение по обеим перемычкам, т.е. по элементам 3 и 6.