Виды резервирования

• структурное - использование избыточных элементов, входящих в физическую структуру объекта;

• временное - использование избыточного времени, выделенного для выполнения задач;

• информационное - использование избыточной информации сверх минимально необходимой для выполнения задач;

• функциональное - использование способности элементов выполнять дополнительные функции вместо основных или наряду с ними;

• нагрузочное - использование способности элементов воспринимать дополнительные нагрузки сверх минимальных;

• смешанное - сочетание различных видов резервирования в одном и том же объекте.

По уровню резервирование может быть:

• общее - резервирование объекта в целом;

• раздельное - резервирование отдельных элементов или их групп.

Сравнение общего и раздельного резервирования

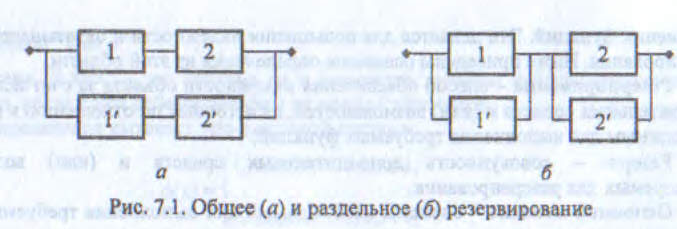
Проведем сравнение наработки до отказа системы при общем и раздельном резервировании (рис. 7.1, для сокращения записи считаем, что число элементов равно двум). Обозначим:

ξ₁ и ξ₂ - наработки до отказа основных элементов,

ξ₁’ и ξ₂’ - наработки до отказа резервных элементов,

ξo и ξp -наработки до отказа системы при общем и раздельном резервировании.

При нагруженном резервировании:

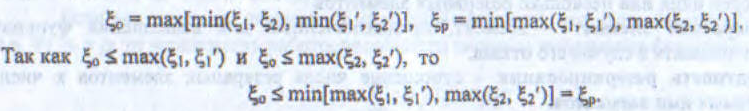
При ненагруженном резервировании:

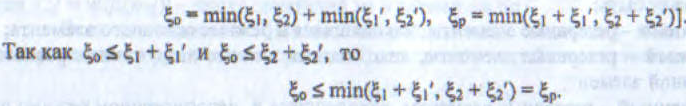
Таким образом, в обоих случаях раздельное резервирование обеспечивает большую надежность, чем общее. Аналогичный результат может быть доказан не только для наработки, но и для вероятности работоспособности.

Однако приведенные выше рассуждения не учитывали надежность устройств, которые могут быть необходимы для контроля работоспособности элементов и переключения на резерв. Если они не абсолютно надежны, сделанный вывод может оказаться и неверным. Например, в рассмотренном случае при общем резервировании нужен только один переключатель, а при поэлементном - два (и их число будет увеличиваться с ростом числа элементов в системе). Поэтому в общем случае требуется более сложный расчет, который приводит к разным результатам в зависимости от надежности контрольно-переключающих устройств.

13. Дублированная система: расчет надежности с помощью марковских процессов (нагруженный и ненагруженный резерв, ограниченное и неограниченное восстановление)

Дублирование является простейшим и широко распространенным на практике случаем резервирования. Система состоит из двух одинаковых элементов: основного и резервного. Предполагается, что длительности безотказной работы элементов имеют экспоненциальное распределение с параметром λ, а длительности восстановления -экспоненциальное распределение с параметром µ. Данное предположение позволяет описать поведение системы марковским случайным процессом.

Рассмотрим два варианта резервирования:

• нагруженное - интенсивность отказов резервного элемента равна интенсивности отказов основного;

• ненагруженное - до момента отказа основного элемента резервный элемент отказать не может, т.е. интенсивность его отказов при нахождении в резерве равна нулю;

и два варианта восстановления:

• неограниченное - при отказах обоих элементов они восстанавливаются одновременно и независимо;

• ограниченное - одновременно может восстанавливаться только один элемент.

Заметим, что в случае нагруженного резерва и неограниченного восстановления система представляет собой просто два параллельных независимых элемента. Во всех остальных случаях элементы зависимы (по отказам или восстановлению).

Состояния системы различаются числом отказавших элементов (0, 1 или 2) и обозначаются «0», «1» и «2» соответственно. Диаграмма состояний и переходов между ними представлена на рис. 7.2.

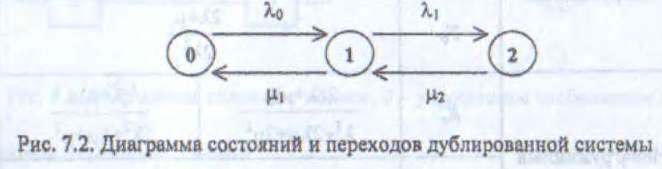
Интенсивности переходов определяются следующими выражениями:

(13.1 – 13.2)

Пусть - вероятность того, что в момент времени t система находится в состоянии j (j=0,1,2). При t->∞ эти вероятности стремятся к своим стационарным значениям, обозначаемым . На практике, как правило, используются именно стационарные характеристики системы.

Поскольку дублированная система неработоспособна только в состоянии «2», коэффициент простоя системы равен стационарной вероятности пребывания в этом состоянии , а среднее время восстановления системы , есть среднее время пребывания в этом состоянии . Коэффициент готовности и средняя наработка на отказ системы (K и ) находятся из и . Таким образом,

(13.3)

Для стационарных вероятностей имеет место система уравнений равновесия:

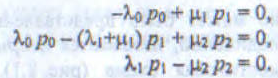
Каждое из уравнений этой системы является следствием двух других, поэтому, взяв любые два уравнения и добавив к ним условие нормировки

получим для систему трех линейных уравнений с тремя неизвестными, решение которой легко находится (например, методом исключения или по правилу Крамера). В частности,

Подставляя сюда значения , , из (13.1) и (13.2), а затем, используя (13.3), получим результаты для четырех возможных случаев, представленных в таблице:

Резерв	Показатель	Восстановление
		неограниченное	ограниченное
Нагруженный	Кг
	То
Ненагруженный	Кг
	То

Аналогично могут быть проанализированы системы с резервированием большей кратности, другими вариантами резервирования. Например, с облегченным резервом, при котором интенсивность отказов резервного элемента λ' удовлетворяет условию 0 < λ ' < λ (в случае нагруженного резерва λ ' = λ, ненагруженного - λ ' = 0).