
- •Донецьк 2010
- •Введение
- •1. Моделирование рядов динамики
- •1.1. Определение параметров моделирующих функций
- •1.2. Оценка адекватности и надежности модели
- •1.3. Оценка параметров уравнений
- •1.4. Использование моделей тренда в прогнозировании
- •2. Автокорреляция уровней динамического ряда
- •Свойства коэффициента автокорреляции:
- •3. Автокорреляция остатков
- •3.1. Критерий Дарбина – Уотсона (d - статистика)
- •Ограничения на применение критерия Дарбина - Уотсона:
- •3.2. Нециклический коэффициент автокорреляции остатков
- •3.3.Циклический коэффициент автокорреляции остатков
- •4.2. Снижение влияния гетероскедастичности
- •5 Множественная регрессия
- •5.1. Классический подход
- •Расчет элементов коэффициента
- •Коэффициенты эластичности результативного показателя по факторам определяются по формуле (51)
- •5.2. Матричный подход
- •5.3. Расчеты с использованием пк
- •Вывод итогов
- •6 Мультиколлинеарность
- •7 Ранговая корреляция
- •7.1. Экспертное оценивание
- •7.2. Этапы работ в системе экспертных оценок
- •7.3. Метод ранговой корреляции
- •Вспомогательные расчеты
- •Б) Случай многих экспертов
- •8 Сетевое планирование
- •9. Компьютерная поддержка расчетов в пакете Excel
- •9.1. Ввод данных
- •9.2. Построение расчетной таблицы
- •9.3. Вычисление параметров моделирующих уравнений
- •9. 4. Графическое представление данных
- •Данных диаграммы
- •Параметры диаграммы
- •Размещение диаграммы
- •9.5. Построение линии тренда
- •9.6. Использование опции Мастер функций
- •9.7. Использование пакета Анализ данных
- •Литература
- •Коэффициентов автокорреляции
- •Критические значения и для коэффициента автокорреляции критерия Дарбина-Уотсона для
- •Критические значения и для коэффициента автокорреляции критерия Дарбина-Уотсона для
- •Значение критерия Пирсона
- •Квантили распределения Стьюдента
3.2. Нециклический коэффициент автокорреляции остатков
Уровень
автокорреляции
остатков измеряют также с помощью
нециклического коэффициента автокорреляции,
который характеризует тесноту связи
остатков каждого последующего значения
с предыдущим, а именно, ряда
![]() с рядом
с рядом
![]() .
Нециклический коэффициент корреляции
вычисляется по формуле [1]:
.
Нециклический коэффициент корреляции
вычисляется по формуле [1]:
 (36)
(36)
Если
![]() то получим отрицательную автокорреляцию
остатков, если
то получим отрицательную автокорреляцию
остатков, если
![]() - положительную. Если
- положительную. Если
![]() ,
то автокорреляция остатков отсутствует.
Однако, не всегда можно установить
вероятностный характер
,
то автокорреляция остатков отсутствует.
Однако, не всегда можно установить
вероятностный характер
![]() ,
поэтому чаще используют циклический
коэффициент автокорреляций.
,
поэтому чаще используют циклический
коэффициент автокорреляций.
3.3.Циклический коэффициент автокорреляции остатков
Циклический
коэффициент автокорреляции остатков
характеризует тесноту связи рядов
и
,
![]() и вычисляется по формуле [1]:
и вычисляется по формуле [1]:
 (37)
(37)
Для того, чтобы
сделать вывод о наличии автокорреляции
остатков фактическое значение циклического
коэффициента автокорреляции
![]() сравнивают
с критическим (табличным) для заданного
числа наблюдений
сравнивают
с критическим (табличным) для заданного
числа наблюдений
![]() и уровня значимости
и уровня значимости
![]() (см. Приложение 1). Если
(см. Приложение 1). Если
![]() то можно утверждать, что автокорреляция
остатков присутствует. В противном
случае автокорреляция остатков
отсутствует.
то можно утверждать, что автокорреляция
остатков присутствует. В противном
случае автокорреляция остатков
отсутствует.
Пример 3.2. |
Проверить гипотезу о наличии автокорреляции остатков с помощью циклического коэффициента автокорреляции для линейной функции, построенной в примере 1.1. |
Решение. |
Линейная функция, которая была построена в примере 1.1, имеет вид
Исходные данные, значения остатков и результаты промежуточных расчетов представлены в таблице 3.2. |
Таблица 3.2
х |
|
|
|
|
|
|
1 |
14.6 |
14.9658 |
-0.3658 |
|
|
0.13381 |
2 |
15.5 |
15.9016 |
-0.4016 |
-0.3658 |
0.1469 |
0.16128 |
3 |
17.0 |
16.8374 |
0.1626 |
-0.4016 |
-0.0653 |
0.02644 |
4 |
18.7 |
17.7732 |
0.9268 |
0.1626 |
0.15069 |
0.85896 |
5 |
18.8 |
18.709 |
0.091 |
0.9268 |
0.08434 |
0.008281 |
6 |
19.8 |
19.6448 |
0.1552 |
0.091 |
0.01412 |
0.024087 |
7 |
20.1 |
20.5806 |
-0.4806 |
0.1552 |
-0.07459 |
0.23098 |
8 |
21.5 |
21.5164 |
-0.0164 |
-0.4806 |
0.007882 |
0.000269 |
9 |
22.8 |
22.4522 |
0.3478 |
-0.0164 |
-0.005704 |
0.12097 |
10 |
23.0 |
23.388 |
-0.388 |
0.3478 |
-0.13495 |
0.15054 |
|
|
|
0.031 |
|
0.123388 |
1.7156 |
По формуле (37) рассчитаем циклический коэффициент автокорреляции остатков:

Зададим уровень
значимости
.
По таблицам определим критическое
значение коэффициента автокорреляции
![]() .
.
![]() .
Поскольку
.
Поскольку
![]() , то автокорреляция остатков отсутствует,
что согласуется с результатом примера
3.1.
, то автокорреляция остатков отсутствует,
что согласуется с результатом примера
3.1.
4. Гетероскедастичность
Так
как каждая конкретная выборка данных
не содержит информации о дисперсиях
ошибок, то исследователю приходится
задавать функциональные зависимости
для этих дисперсий. Наиболее часто
используется графический анализ остатков
и тест Голдфельда – Квандта.![]()
Графический анализ остатков
Это
наиболее простой и наглядный способ
обнаружения гетероскедастичности.
После нахождения теоретической
зависимости модели
![]() строится график остатков регрессии
строится график остатков регрессии
![]() или их квадратов
или их квадратов
![]() .
Если разброс отклонений
равномерный (находится внутри полосы
постоянной ширины), то модель
гомоскедастична. Изменение ширины
полосы разброса остатков свидетельствует
о наличии гетероскедастичности (см.
рисунок 3.2).
.
Если разброс отклонений
равномерный (находится внутри полосы
постоянной ширины), то модель
гомоскедастична. Изменение ширины
полосы разброса остатков свидетельствует
о наличии гетероскедастичности (см.
рисунок 3.2).
4.1 Тест Голдфельда – Квандта
Этот
тест является вероятностным тестом
статистической проверки гипотезы Но
об
отсутствии гетероскедастичности или
гипотезы Н1
–
о ее наличии. Он базируется на предположении
о пропорциональной зависимости между
стандартным отклонением
![]() и значениями фактора хі,
т.е.
и значениями фактора хі,
т.е.
![]() Очевидно, в этом случае следует ожидать,
что сумма квадратов
Очевидно, в этом случае следует ожидать,
что сумма квадратов
![]() в
начале выборки будет значительно меньше,
чем в конце выборки. Кроме того,
предполагается нормальное распределение
остатков
и отсутствие автокорреляции остатков
в
начале выборки будет значительно меньше,
чем в конце выборки. Кроме того,
предполагается нормальное распределение
остатков
и отсутствие автокорреляции остатков
![]()
Алгоритм выполнения теста Голдфельда – Квандта
Выборка упорядочивается в порядке возрастания .
Четверть средних элементов выборки отбрасывается (множество В2), после чего первые
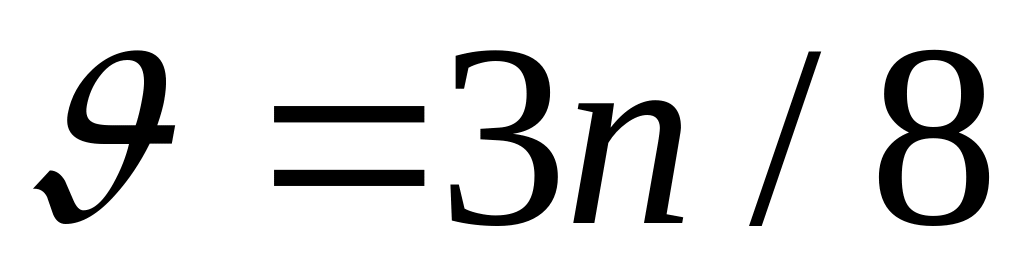 элементов образуют выборку В1
, а последние
элементов образуют выборку В1
, а последние
 элементов – выборку В3.
элементов – выборку В3.Для выборок В1 и В3 строятся две линейные модели, определяются остатки и находятся их суммы
 и
и
 .
.Определяется F-статистика значимости гипотезы Но об отсутствии гетероскедастичности
 .
.По таблице критических значений F- статистики (см. Приложение 4) с уровнем значимости и числом степеней свободы
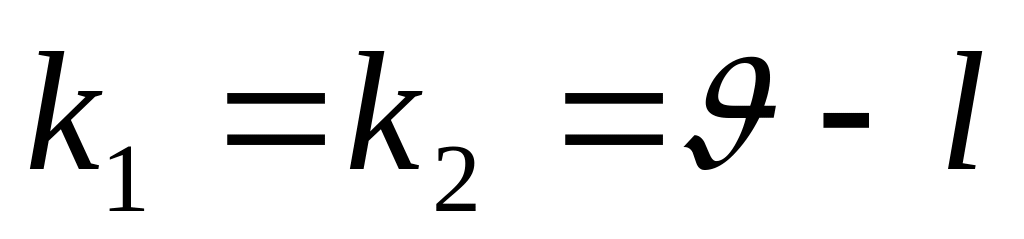 находится
критическое значение
находится
критическое значение
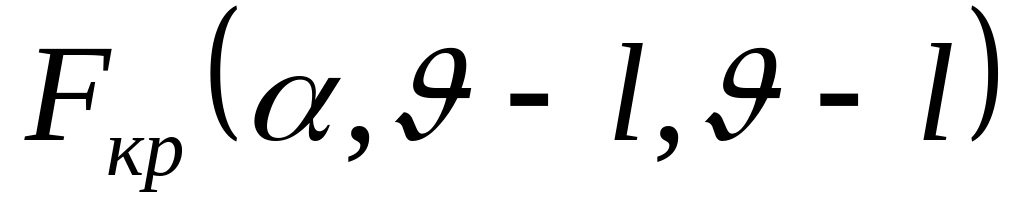 .
.При F > Fкр гипотеза Но об отсутствии гетероскедастичности отвергается и принимается гипотеза Н1 – гетероскедастичность присутствует. В противном случае принимается гипотеза Но.
Пример 4.1 |
Данные по товарообороту торгового предприятия за 24 месяца приведены в таблице 4.1. |
Таблица 4.1
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
5,2 |
7,1 |
6,5 |
6 |
8 |
7 |
6,1 |
9 |
7,2 |
10,7 |
7 |
11 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
|
8,2 |
10,7 |
9 |
13,4 |
11,9 |
8,8 |
10 |
14 |
10,1 |
9 |
16,8 |
14 |
Используя тест Голдфельда – Квандта, определить в линейной модели наличие или отсутствие гетероскедастичности.
Решение. |
Рассмотрим
выборку объема
|

Рисунок 4.1 – Линейный тренд для полной выборки
Таблица 4.2
|
|
|
|
|
|
3 |
5,2 |
5,973333 |
-0,77333 |
0598044 |
|
4 |
7,1 |
6,205 |
0,895 |
0,801025 |
|
5 |
6,5 |
6,436667 |
0,06333 |
0,004011 |
|
6 |
6 |
6,668333 |
-0,66833 |
0,446669 |
|
7 |
8 |
6,9 |
1,1 |
1,21 |
|
8 |
7 |
7,131667 |
-0,1367 |
0,017336 |
|
9 |
6,1 |
7,363333 |
-1,2633 |
1,596011 |
|
10 |
9 |
7,595 |
1,405 |
1,974025 |
|
11 |
7,2 |
7,826667 |
-0,62667 |
0,392711 |
7,039833 |
12 |
10,7 |
|
|
|
|
13 |
7 |
|
|
|
|
14 |
11 |
|
|
|
|
15 |
8,2 |
|
|
|
|
16 |
10,7 |
|
|
|
|
Продолжение таблицы 4.2
17 |
9 |
|
|
|
|
18 |
13,4 |
10,82667 |
2,57333 |
6,622044 |
|
19 |
11,9 |
11,12 |
0,78 |
0,6084 |
|
20 |
8,8 |
11,41333 |
-2,61333 |
6,829511 |
|
21 |
10 |
11,70667 |
-1,70667 |
2,912711 |
|
22 |
14 |
12 |
2 |
4 |
|
23 |
10,1 |
12,29333 |
-2,19333 |
4,810711 |
|
24 |
9 |
12,58667 |
-3,58667 |
12,86418 |
|
25 |
16,8 |
12,88 |
3,92 |
15,3664 |
|
26 |
14 |
13,17333 |
0,826667 |
0,683378 |
54,69733 |
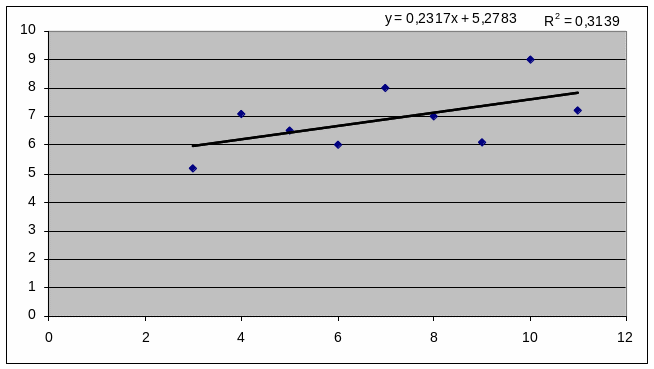
Рисунок 4.2. – Линейный тренд для выборки В1

Рисунок 4.3. – Линейный тренд для выборки В3
Вычислим
остатки
,
их квадраты
и суммы квадратов
![]() и
и
![]() .
Результаты расчетов приведены в таблице
4.2.
.
Результаты расчетов приведены в таблице
4.2.
Определим F- статистику
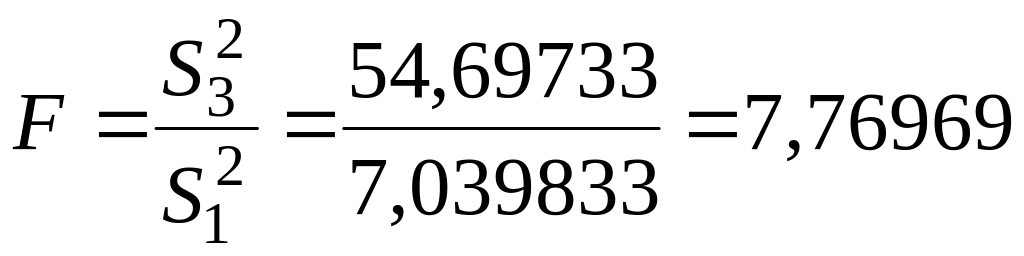 .
.
По
таблице критических точек распределения
Фишера (Приложение 2) при
![]() находим Fкр=3,79.
Так как F >Fкр
с доверительной вероятностью 95% гипотеза
Но отвергается,
то есть гетероскедастичность в данной
выборке имеет место.
находим Fкр=3,79.
Так как F >Fкр
с доверительной вероятностью 95% гипотеза
Но отвергается,
то есть гетероскедастичность в данной
выборке имеет место.
