3.5. Сравнение двух средних генеральных совокупностей

1) Генеральные совокупности Х и Y распределены нормально, причем известны их дисперсии. Из этих генеральных совокупностей извлечены выборки объемов соответственно т и п, для которых найдены выборочные средние и . При заданном уровне значимости α проверяется нулевая гипотеза о равенстве математических ожиданий генеральных совокупностей:

Н_о: М (Х) = М (Y).

Статистическим критерием для проверки этой гипотезы является нормиро-ванная нормально распределенная случайная величина

Наблюдаемое значение критерия . Вид критической области зависит от типа конкурирующей гипотезы:

а) Н₁: М (Х) ≠ М (Y) – критическая область двусторонняя, z_кр определяется как аргумент функции Лапласа, при котором и критическая область задается неравенством |Z| > z_кр.

б) Н₁: М (Х) > М (Y) – критическая область правосторонняя, z_кр определяется как аргумент функции Лапласа, при котором и критическая область определяется неравенством Z > z_кр.

в) Н₁: М (Х) < М (Y) – критическая область левосторонняя, заданная неравен-ством Z < -z_кр, где z_кр вычисляется так же, как в предыдущем случае.

2) Имеются две независимые выборки большого объема, извлеченные из генеральных совокупностей, законы распределения и дисперсии которых неизвестны. При этом для объема выборки, не меньшего 30, можно считать, что выборочные средние распределены приближенно нормально, а выборочные дисперсии являются достаточно хорошими оценками генеральных дисперсий (следовательно, считаем известными приближенные значения генеральных дисперсий). Тогда задача сводится к предыдущей, и статистический критерий имеет вид:

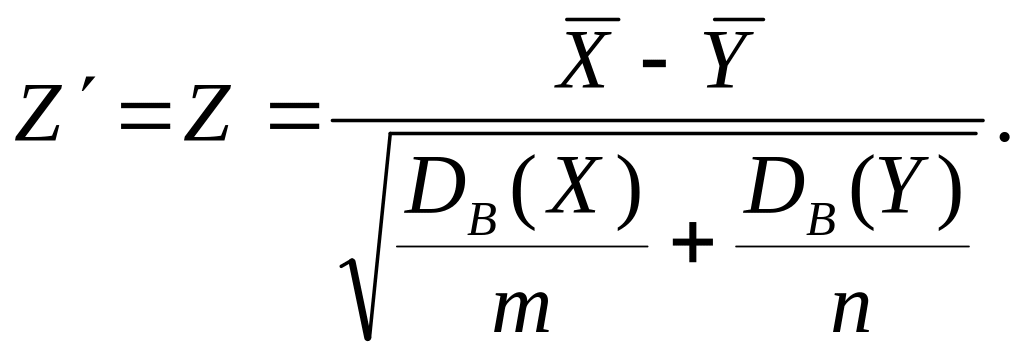
Наблюдаемое значение критерия вычисляется по формуле

При этом выбор вида критической области и определение критических точек проводятся так же, как в пункте 1.

3) Генеральные совокупности распределены нормально, причем их дисперсии неизвестны, а объем выборок т и п мал (следовательно, нельзя получить хорошие оценки генеральных дисперсий). Если предположить, что генеральные дисперсии равны, то в качестве критерия для проверки нулевой гипотезы Н_о: М (Х) = М (Y) служит случайная величина

,

имеющая при справедливости нулевой гипотезы распределение Стьюдента с k = n + m – 2 степенями свободы. Наблюдаемое значение критерия вычисляется по формуле

.

Критическая область строится в зависимости от вида конкурирующей гипотезы.

а) Н₁: М (Х) ≠ М (Y) – критическая область двусторонняя, задаваемая неравенством |T| > t_{двуст.кр.}, где t_{двуст.кр.}(α, k) находится из таблицы критических точек распределения Стьюдента.

б) Н₁: М (Х) > М (Y) – критическая область правосторонняя, определяемая условием T > t_{прав.кр.}. Критическая точка вновь находится по таблице критических точек распределения Стьюдента.

в) Н₁: М (Х) < М (Y) – критическая область левосторонняя, T < – t_{прав.кр.}.

Пример. Имеются независимые выборки значений нормально распределенных случайных величин

Х: 2, 2, 3, 3, 4, 4, 4, 5, 5, 6 и Y: 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 7, 8, 9.

Требуется проверить для уровня значимости α = 0,1 при условии равенства генеральных дисперсий нулевую гипотезу Н_о: М (Х) = М (Y) при конкурирующей гипотезе Н₁: М (Х) ≠ М (Y).

Объемы выборок т = 10, п = 15. Вычислим выборочные средние и исправленные выборочные дисперсии: Вычислим наблюдаемое значение критерия: Критическая область – двусторонняя, t_{двуст.кр.}(0,1; 23) = 1,71 (см. [2], приложение 6). Итак, |T_набл | < t_{двуст.кр.}, следовательно, нет оснований отвергнуть нулевую гипотезу – можно считать, что математические ожидания генеральных совокупностей равны. ◄