24. Замечательные пределы

n^o1. Первый замечательный предел и его следствия.Покажем, что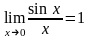 (первый замечательный предел),т.е., что

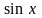~ ( ).(Так как функция 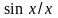– четная, то достаточно найти правосторонний ее предел в точке .

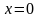Пусть 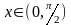. Тогда как видно из следующего рисунка )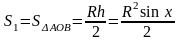 , ,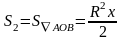 ,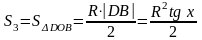при этом ясно, что 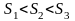.Поэтому

и, следовательно,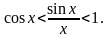 Таким образом, если будет доказано, что 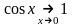,то будет доказано и (1).Используя левое из неравенств (2) получим ,а так как ,то из этих неравенств в силу принципа двух милиционеров получим (3). а следовательно и (1).Как следствие (1) и (3) имеем 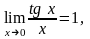В свою очередь из (1) и (4) следует что 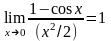Таким образом, 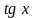~ , а ~ при .

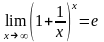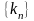n^o2. Второй замечательный предел Имеет место равенство (7)Покажем сначала, что (8) (Действительно, так как ,то для любой последовательности натуральных чисел такой, что имеем (9) Но для любой последовательности вещественных чисел

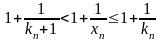где , и, следовательно, .

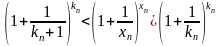Поэтому, если , то и в силу (9) и принципа двух милиционеров, для любой последовательности вещественных чисел , такой, что имеем также

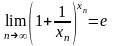.По определению предела в смысле Гейне это и означает, что справедливо равенство (8). Используя его и теорему о пределе суперпозиции легко убедиться также и в том, что(10)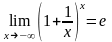 Наконец (7) следует из (8) и (10).

17. Критерий Коши существования предела функции

Теорема (критерий Коши). Пусть функция определена на множестве и (конечная или бесконечная) точка сгущения этого множества. Для того, чтобы существовал предел

необходимо и достаточно, чтобы существовала такая окрестность точки , что для любых

.

(2)

25. Асимптоты графика функции

Определение1. Прямая 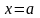называется вертикальной асимптотой графика функции , если хотя бы один из пределов

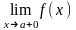или

равен или .

Определение 2. Прямая называется наклонной асимптотой графика функции пр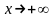и ( ), если

( ).	(1)
Теорема. Для того, чтобы прямая была наклонной асимптотой графика функции при ( ), необходимо и достаточно, чтобы ( ).		(2)

Д о к а з а т е л ь с т в о . Пусть, например, - наклонная асимптота графика функции при . Тогда из равенств

в силу (1) следует (2). Необходимость доказана.

Докажем достаточность. Действительно, если имеют равенства (2), то из второго из них следует (1), т.е. - наклонная асимптота графика функции при □

26. Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела

Определение 1. Функция , , называется непрерывной в точке 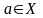, если для любого существует такое , что для любого , удовлетворяющего неравенству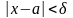

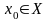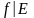Теорема 1 (О непрерывности сужения). Пусть функция непрерывна в точке и причем . Тогда функция также непрерывна в точке .

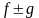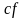
Теорема 2 (Арифметические свойства непрерывных функций). Пусть функции и определены на множестве и непрерывны в точке . Тогда и функции: , , 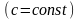, 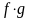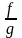(при на )

непрерывны в точке .

Теорема 3 (О локальной ограниченности). Пусть функция определена на множестве и непрерывна в точке . Тогда если – точка сгущения множества , то существует такая окрестность точки , что функция ограничена на множестве .

Теорема 4 (О стабилизации знака). Пусть функция определена на множестве и непрерывна в точке . Тогда если и – точка сгущения множества , то существует такая окрестность точки , что .

Теорема 5. Пусть функция определена на множестве и непрерывна в точке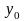 , а функция определена на множестве и непрерывна в точке , причем 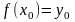и . Тогда сложная функция непрерывна в точке .

Теорема 6. Функция непрерывна в точке она непрерывна в ней слева и справа одновременно.
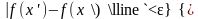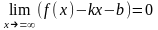