
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •10. Число e.
- •11. Бесконечно малые и бесконечно большие последовательности.
- •12. Лемма о вложенных отрезках.
- •18. Локальные свойства функций имеющих предел.
- •16. Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности
- •21. Бесконечные пределы и пределы в бесконечности.
- •19.Теорема о пределе суперпозиции
- •23. Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •24. Замечательные пределы
- •27. Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •29. Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •30. Теоремы Вейерштрасса о непрерывных на отрезке функциях
- •Д о к а з а т е л ь с т в о. Достаточно заметить, что
- •33. Дифференцируемые функции. Понятие дифференциала
- •46. Условия монотонности функции.
- •47. Условия экстремума функции.
- •48. Условия выпуклости функции
- •51.Комплексные числа
- •14. Частичные пределы. Верхний и нижний пределы.
- •13. Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •28. Равномерно непрерывные функции. Теорема Кантора.
- •40. Производные и дифференциалы высших порядков.
- •39. Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
18. Локальные свойства функций имеющих предел.
Определение
1. Пусть
функция
определена на множестве
 и
и
 – некоторое его подмножество (
– некоторое его подмножество ( ).
Говорят, что функция
ограничена (соотв., ограничена сверху
или снизу) на множестве
,
если его образ
).
Говорят, что функция
ограничена (соотв., ограничена сверху
или снизу) на множестве
,
если его образ
 есть ограниченное (соотв., ограниченное
сверху или снизу) множество.
есть ограниченное (соотв., ограниченное
сверху или снизу) множество.
Теорема
1
(о
локальной ограниченности).
Пусть
функция
определена на множестве
и
- точка сгущения этого множества. Тогда
если существует предел
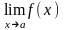 ,
то
существует такая окрестность
,
то
существует такая окрестность
 точки
,
что функция
ограничена
на множестве
точки
,
что функция
ограничена
на множестве
 .
.
Ниже
знак числа
обозначается через
 .
.
Теорема
2
(о
стабилизации знака).
Пусть
функция
определена на множестве
и
- точка сгущения этого множества.
Тогда если существует отличный от
нуля предел
|
|
16. Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности
Числовой
функцией или функцией одной (вещественной)
переменной называется отображение
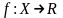 ,
область определения которой есть
числовое множество, т.е.
.
,
область определения которой есть
числовое множество, т.е.
.
Пусть
и
– окрестность точки
.
Множество
 далее будем называть проколотой
окрестностью
точки
.
далее будем называть проколотой
окрестностью
точки
.
Определение
1. Точка
называется точкой
сгущения
или
предельной
точкой
множества
,
если в любой ее проколотой окрестности
имеется хотя бы одна точка этого
множества, т.е. если для любой окрестности
точки
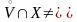 Æ.
Æ.
Определение
2 (предела
функции по Коши).
Пусть функция
определена на множестве
и
– точка сгущения этого множества. Число
 называется пределом
функции
при
называется пределом
функции
при
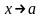 или, также, пределом
функции
в
точке
,
если для любого
существует такое
или, также, пределом
функции
в
точке
,
если для любого
существует такое
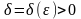 ,
что для любого
,
удовлетворяющего неравенствам:
,
что для любого
,
удовлетворяющего неравенствам:
|
|
имеет место неравенство
|
(2) |
Определение 2’. Пусть функция определена на множестве и – точка сгущения этого множества. Число называется пределом функции при или, также, пределом функции в точке , если для любого существует такое , что
.
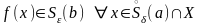 .
.
Определение
3 (предела
по Гейне).
Пусть
функция
определена на множестве
и
– точка сгущения этого множества. Число
называется пределом
функции
при
или, также, пределом
функции
в точке
,
если для любой последовательности
 последовательность
последовательность
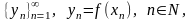 сходится и
сходится и
|
(3) |
Теорема 1. Определения предела функции по Коши и по Гейне равносильны.
Теорема
2.
Если функция
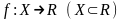 имеет предел в точке
,
где
– точка сгущения множества
,
то этот предел единственный
имеет предел в точке
,
где
– точка сгущения множества
,
то этот предел единственный
Теорема
3 (об
арифметических свойствах предела
функции). Пусть
функции
и
определены на множестве
и
- точка сгущения этого множества. Тогда
если существуют пределы
и
 ,то
существуют и пределы
,то
существуют и пределы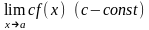 ,
,
 ,
,
 ,
,
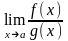 (последний
при дополнительном предположении, что
и
(последний
при дополнительном предположении, что
и
 ),причем
),причем
а)

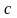 ,
,
б)
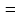
 (теорема
о пределе суммы и разности),
(теорема
о пределе суммы и разности),
в) (теорема о пределе произведения),
г)
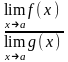 (теорема о пределе частного).
(теорема о пределе частного).
Теорема
4
(о предельном переходе в неравенстве).
Пусть
функции
и
определены на множестве
и
- точка сгущения множества
.
Тогда если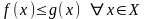 и
существуют пределы
и
,
то
.
и
существуют пределы
и
,
то
.
Теорема 5 (принцип двух милиционеров). Пусть функции , и
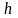 определены
на множестве
и
- точка сгущения множества
.
Тогда если
определены
на множестве
и
- точка сгущения множества
.
Тогда если
 и
существуют равные между собой пределы
и
и
существуют равные между собой пределы
и
 ,то
существует и равный им предел
,т.е.
.
,то
существует и равный им предел
,т.е.
.
20. Односторонние пределы.
Пусть задана функция и точка . Рассмотрим множества
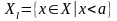 и
и .
.
Определение
1.
Пусть
- точка сгущения множества
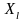 .
Если
.
Если
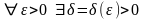 такое, что
такое, что
 ,
удовлетворяющего неравенствам
,
удовлетворяющего неравенствам
 имеет
место неравенство
.
то число
называется левосторонним
пределом функции
в точке
или также пределом
функции
в
точке
слева.
имеет
место неравенство
.
то число
называется левосторонним
пределом функции
в точке
или также пределом
функции
в
точке
слева.
Определение
2.
Пусть
- точка сгущения множества
 .
Если
такое, что
,
удовлетворяющего неравенствам
.
Если
такое, что
,
удовлетворяющего неравенствам
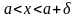 имеет
место неравенство
то число
называется правосторонним
пределом
функции
в
точке
,
или также пределом
функции
в
точке
справа
имеет
место неравенство
то число
называется правосторонним
пределом
функции
в
точке
,
или также пределом
функции
в
точке
справа
Теорема
1.
Пусть
,
и
–
точка
сгущения
каждого из множеств
и
.
Тогда,
если существуют равные между собой
односторонние пределы и
и
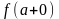 ,
то
существует и равный им двусторонний
предел
=
=
.
,
то
существует и равный им двусторонний
предел
=
=
.

 ,
то
в некоторой проколотой окрестности
точки
функция
имеет тот же знак, что и этот предел:
точнее, существует такая окрестность
точки
,
что
,
то
в некоторой проколотой окрестности
точки
функция
имеет тот же знак, что и этот предел:
точнее, существует такая окрестность
точки
,
что
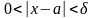
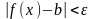

 .
.