
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •10. Число e.
- •11. Бесконечно малые и бесконечно большие последовательности.
- •12. Лемма о вложенных отрезках.
- •18. Локальные свойства функций имеющих предел.
- •16. Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности
- •21. Бесконечные пределы и пределы в бесконечности.
- •19.Теорема о пределе суперпозиции
- •23. Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •24. Замечательные пределы
- •27. Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •29. Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •30. Теоремы Вейерштрасса о непрерывных на отрезке функциях
- •Д о к а з а т е л ь с т в о. Достаточно заметить, что
- •33. Дифференцируемые функции. Понятие дифференциала
- •46. Условия монотонности функции.
- •47. Условия экстремума функции.
- •48. Условия выпуклости функции
- •51.Комплексные числа
- •14. Частичные пределы. Верхний и нижний пределы.
- •13. Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •28. Равномерно непрерывные функции. Теорема Кантора.
- •40. Производные и дифференциалы высших порядков.
- •39. Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
21. Бесконечные пределы и пределы в бесконечности.
Определения.
1.
Окрестностью
точки
в
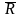 (как и ранее) называется всякое множество
(как и ранее) называется всякое множество
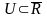 ,
которое содержит некоторую
-окрестность
,
которое содержит некоторую
-окрестность
 этой точки.
этой точки.
2.
Окрестностью
точки
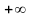 в
называется
любой промежуток вида
в
называется
любой промежуток вида
 ,
где
.
,
где
.
3.
Окрестностью
точки
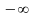 в
называется любой промежуток вида
в
называется любой промежуток вида
 ,
где
.
,
где
.
4.
Пусть
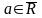 и
–окрестность
этой точки (в
).
Тогда множество
и
–окрестность
этой точки (в
).
Тогда множество
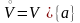 называется
проколотой
окрестностью точки
.
называется
проколотой
окрестностью точки
.
5.
Точка
называется точкой
сгущения множества
,
если для любой окрестности
этой точки
 Æ.
Æ.
Определение
6. Пусть
– конечная и ли бесконечная точка
сгущения множества
и функция
определена на множестве
.
Конечное или бесконечное число (точка)
 называется пределом
функции
при
(или
в
точке
),
если для любой окрестности
называется пределом
функции
при
(или
в
точке
),
если для любой окрестности
 точки
точки
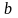 (в
)
существует такая окрестность
(в
)
существует такая окрестность
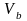 точки
(в
),
что
точки
(в
),
что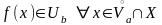 .
.
Замечание 1. Для различных типов точек и определение 5 с учетом определения их окрестностей можно сформулировать в терминах неравенств:
А)

 :
: .
.
Б)
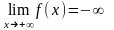
 :
:

В)
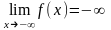 :
:
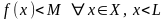
Г)
 :
:

Д)
 (
)
(
) :
:
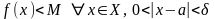
Е)
 (
)
:
(
)
:
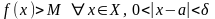
Ж)
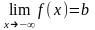 (
)
(
)
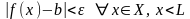
З)
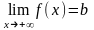 (
)
(
)
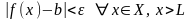
19.Теорема о пределе суперпозиции
Теорема
(о
пределе суперпозиции).
Пусть
функция
определена на множестве
,
|
|
|
Пусть,
кроме того, функция
определена на множестве
|
|
|
Тогда,
если |
(3) |
|
то
на множестве
|
(4) |
|
22. Бесконечно малые и бесконечно большие функции
Определение
1.
Пусть функция
определена на множестве
и
- его точка сгущения. Функция
называется бесконечно малой при
если
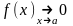 .
.
Теорема 1. Сумма любого конечного числа бесконечно малых при функций есть бесконечно малая при функция.
Теорема 2. Произведение бесконечно малой при функции и ограниченной в окрестности точки функции является бесконечно малой при функцией.
Определение
2. Пусть
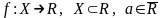 –
точка сгущения множества
.
Функция
называется бесконечно
большой при
,
если
–
точка сгущения множества
.
Функция
называется бесконечно
большой при
,
если
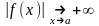 .
.
Теорема
3 (о
связи между бесконечно малыми и
бесконечно большими). Пусть
- точка сгущения множества
и
 на
(или,
хотя бы, в некоторой окрестности точки
).
Тогда,если
– бесконечно малая при
функция, то
на
(или,
хотя бы, в некоторой окрестности точки
).
Тогда,если
– бесконечно малая при
функция, то
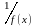 – бесконечно большая при
функция;если же
– бесконечно большая при
функция, то
– бесконечно малая при
функция.
– бесконечно большая при
функция;если же
– бесконечно большая при
функция, то
– бесконечно малая при
функция.
23. Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
Опр
1.
Если
 ,то
говорят, что функция
есть о-малое
от
функции
при
,
и пишут
,то
говорят, что функция
есть о-малое
от
функции
при
,
и пишут при
.
при
.
Опр2.
Если
функция
 ограничена
в некоторой проколотой окрестности
ограничена
в некоторой проколотой окрестности
 точки
,
т.е. если она ограничена на множестве
точки
,
т.е. если она ограничена на множестве
 ,
то говорят, что функция
есть
о-большое от функции
при
,
и пишут
,
то говорят, что функция
есть
о-большое от функции
при
,
и пишут при
.
при
.
Опр 3. Пусть и – бесконечно малые при функции. Функция называется бесконечно малой высшего порядка по сравнению с функцией , если при ,т.е. если .
Опр4.
Бесконечно малые при
функции
и
называют эквивалентными
при
и пишут
~
при
,
если
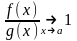
Теор2.
Пусть
 и
и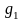 – бесконечно малые при
функции, причем
~
– бесконечно малые при
функции, причем
~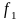 ,
а
~
при
.
Тогда если
,
а
~
при
.
Тогда если
 ,то
и
,то
и
 .
.
Опр7.
Пусть
и
– бесконечно большие при
функции. Функция
называется бесконечно
большой высшего порядка
по сравнению с функцией
,
если
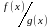 – бесконечно большая при
функция, т.е. если
– бесконечно большая при
функция, т.е. если
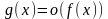 при
.
при
.
8. Если бесконечно большие при функции и асимптотически равны при , то говорят, что они эквивалентны при .

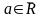 – точка сгущения множества
и существует предел
– точка сгущения множества
и существует предел .
.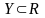 ,
–
точка сгущения множества
и существует предел
,
–
точка сгущения множества
и существует предел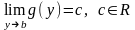 .
. ,
,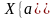 имеет смысл суперпозиция
имеет смысл суперпозиция
 и существует предел
и существует предел .
.