
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •10. Число e.
- •11. Бесконечно малые и бесконечно большие последовательности.
- •12. Лемма о вложенных отрезках.
- •18. Локальные свойства функций имеющих предел.
- •16. Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности
- •21. Бесконечные пределы и пределы в бесконечности.
- •19.Теорема о пределе суперпозиции
- •23. Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •24. Замечательные пределы
- •27. Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •29. Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •30. Теоремы Вейерштрасса о непрерывных на отрезке функциях
- •Д о к а з а т е л ь с т в о. Достаточно заметить, что
- •33. Дифференцируемые функции. Понятие дифференциала
- •46. Условия монотонности функции.
- •47. Условия экстремума функции.
- •48. Условия выпуклости функции
- •51.Комплексные числа
- •14. Частичные пределы. Верхний и нижний пределы.
- •13. Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •28. Равномерно непрерывные функции. Теорема Кантора.
- •40. Производные и дифференциалы высших порядков.
- •39. Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
10. Число e.
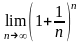 ■Этот
предел обозначают буквой e
и называют числом e.
■Этот
предел обозначают буквой e
и называют числом e.
Лемма
1.
Для
любого
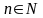 и любого
и любого
 справедливо неравенство
справедливо неравенство
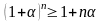 (1)(неравенство
Я. Бернулли)
(1)(неравенство
Я. Бернулли)
Лемма
2.
Существует
предел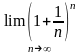 .
.
Доказательство.
Рассмотрим сначала последовательность
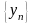 ,
,
 Используя
неравенство
Бернулли,
при
Используя
неравенство
Бернулли,
при
 будем
иметь:
будем
иметь:
 (здесь
³
получено из (1) при
(здесь
³
получено из (1) при
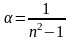 ).
Таким образом,
).
Таким образом,
 и следовательно
и следовательно
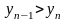 ,
то есть последовательность
- убывающая.Кроме того, очевидно, что
последовательность
положительная
,
то есть последовательность
- убывающая.Кроме того, очевидно, что
последовательность
положительная
 .
Следовательно, она ограничена снизу.
Поэтому существует предел
.
Следовательно, она ограничена снизу.
Поэтому существует предел
 Возвращаясь
к интересующей нас последовательности
Возвращаясь
к интересующей нас последовательности
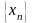 ,
,
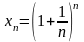 ,видим,
что
,видим,
что
 .Поскольку
существуют пределы:
.Поскольку
существуют пределы: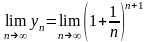 и
и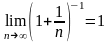 ,то
по теореме о пределе произведения
последовательностей существует и
предел ,
,то
по теореме о пределе произведения
последовательностей существует и
предел , т.е.
предел
■
т.е.
предел
■
Замечание 2. Этот предел обозначают буквой e и называют числом e. Можно доказать, что число e иррациональное. В настоящее время оно вычислено с большей степени точности в частности, в пределах первых пятнадцати знаков после запятой
e = 2,718281828459045…
11. Бесконечно малые и бесконечно большие последовательности.
Определение 1. Последовательность называется бесконечно малой (б.м.), если
 .
.
Теорема 1. Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.
Определение
2.
Если для любого вещественного числа E
$N:xn
> E
"n
> N(соотв.,
xn
< E
"n
> N
),то
говорят, что последовательность
имеет своим пределом
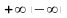 ,
и пишут
,
и пишут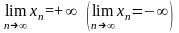 или
или
 .
.
Определение
3.
Последовательность
такую, что
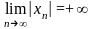 ,
называют бесконечно
большой и
пишут
,
называют бесконечно
большой и
пишут
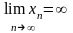 (символ ¥
употребляется без знака).
(символ ¥
употребляется без знака).
Теорема
2.
Если
последовательность
- бесконечно большая и
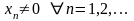 то
то
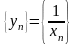 - бесконечно
малая последовательность
- бесконечно
малая последовательность
Теорема
3.
Если
- бесконечно
малая последовательность и
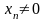 при n
= 1,2,…,
то последовательность
при n
= 1,2,…,
то последовательность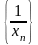 -бесконечно
большая.
-бесконечно
большая.
12. Лемма о вложенных отрезках.
Лемма.
Для
любой последовательности вложенных
отрезков
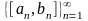 ,
,

(
 ),
),
их пересечение
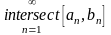 непусто
непусто
Более
того, если длины
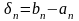 этих отрезков стремятся к нулю
этих отрезков стремятся к нулю
 ,
то это пересечение состоит из одной
точки.
,
то это пересечение состоит из одной
точки.
15. Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
Определение
1.
Последовательность
называется фундаментальной,
если для любого
найдется такой номер
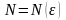 ,
что при всех
,
что при всех
 выполняется неравенство
выполняется неравенство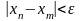 (1)
(1)
Последовательность
называется фундаментальной,
если для любого
найдется такой номер
,
что
и
 справедливо неравенство
справедливо неравенство (1')
(1')
Теорема 1. Если последовательность фундаментальна, то она ограничена.
Док-во:
Пусть фиксировано некоторое
,
тогда существует такой номер N,
что при n,m
> N
выполняется неравенство (1). Возьмем
m
= N
+ 1,
тогда
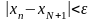 при n
> N
и, следовательно,
при n
> N
и, следовательно,
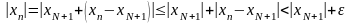 .
.
то
есть все члены последовательности
при n
> N
ограничены числом
 .
.
Положим
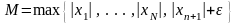 .Очевидно,
.Очевидно,
 при всех
при всех
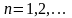 ,
то есть последовательность
ограничена□
,
то есть последовательность
ограничена□
Теорема 2 (Критерий Коши). Для того чтобы последовательность была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.
