13. Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.

Определение. Пусть – произвольная числовая последовательность, – возрастающая последовательность натуральных чисел. Тогда последовательность 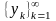, , 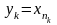, 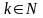называется подпоследовательностью последовательности и обычно обозначается или . Теорема. Всякая подпоследовательность сходящейся последовательности сходится и имеет тот же предел, что и исходная последовательность. Д о к-о. Пусть последовательность сходится и – ее предел. Пусть далее – некоторая подпоследовательность этой последовательности. Выберем произвольное . Так как , то найдется такое ,что 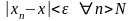,а так как по определению 1 для всякой подпоследовательности 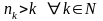,то . В силу произвольности это означает, что □

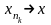Теорема (Больцано-Вейерштрасса).Всякая ограниченная последовательность содержит сходящуюся подпоследовательность.

28. Равномерно непрерывные функции. Теорема Кантора.

Определение 1. Функция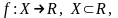 называется непрерывной на множестве , если она непрерывна в каждой точке 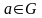.Определение 2. Функция называется равномерно непрерывной на множестве , если для любого такое, что 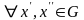, удовлетворяющих неравенству

(1)

имеет место неравенство

.

(2)

Замечание 1. В обоих этих определения не исключается, что 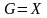Замечание 2. Очевидно, если функция равномерно непрерывна на множестве , то она и непрерывна на нем. Как показывает приводимый ниже пример, обратное утверждение, вообще говоря, неверно, т.е. из непрерывности функции на множестве , вообще говоря, не следует, что она равномерно непрерывна на этом множестве.Замечание 3.Отличие понятия равномерно непрерывной на множестве функции от понятия непрерывной на нем функции состоит в том, что если функция – непрерывна на множестве , то для каждой точки и для каждого существует свое, т.е. зависящее и от , и от точки число , которое для всех , удовлетворяющих неравенству

,

(5)

гарантирует выполнение неравенства

.

(6)

Если же функция – равномерно непрерывна на множестве , то для каждого независимо от выбора точки существует зависящее только от выбранного число , которое для всех , удовлетворяющих неравенству (5), гарантирует выполнение неравенства (6).(Следующая теорема указывает тот важный частный случай, когда из непрерывности функции на множестве следует также и ее равномерная непрерывность на том же множестве).

Теорема 1 (Кантора).Непрерывная на отрезке функция равномерно непрерывна на этом отрезке

40. Производные и дифференциалы высших порядков.

Понятие производной порядка . Пусть функция определена в некоторой окрестности точки и дифференцируема в этой окрестности, т.е. дифференцируема в каждой точке . Тогда в окрестности определена новая функция , которая, называется производной функции на множестве .

общее определение производной порядка если функция имеет в каждой точке конечную производную , то производная функции в точке называется производной -го порядка функции в точке и обозначается одним из символов .

Непосредственно из определения производной -го порядка вытекают следующие ее свойства:

( ) ,где и – раз дифференцируемые в точке функции.

Механический смысл второй производной. Если кинематический закон движения материальной точки вдоль некоторой кривой, т.е. если – путь, пройденный ей вдоль этой кривой к моменту времени из некоторой начальной точки, то, как известно, первая производная , если она существует, представляет собой мгновенную скорость точки в момент времени .Вместе с тем отношение называют средним ускорением точки за отрезок времени , а предел (если он существует) называют ускорением точки в момент времени .

Таким образом вторая производная – ускорение точки в момент времени .

Понятие дифференциала порядка . Пусть функция раз дифференцируема в точке (в соответствии с данным выше определением это означает, напомним, что в некоторой окрестности этой точки она имеет конечные производные до порядка включительно, а в самой точке имеет и конечную производную порядка ). Тогда степенная функция переменной называется дифференциалом функции в точке порядка и обозначается или (короче также пишут или ).Таким образом, для дифференциала порядка функции в точке имеем формулу

,

(1)

При этом понятия дифференциала и первого дифференциала (дифференциала порядка 1) совпадают друг с другом.
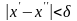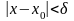