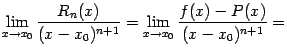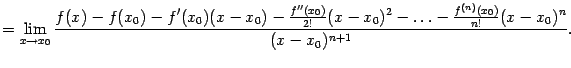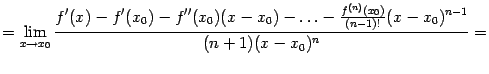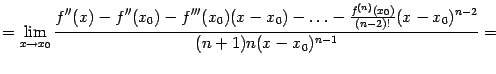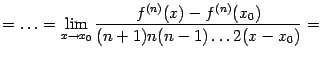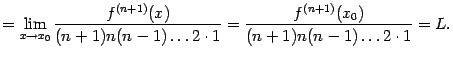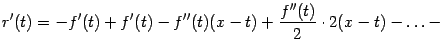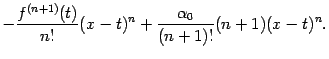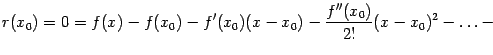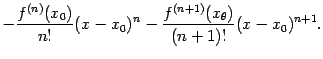Доказательство

Для функции одной переменной:

Введем функцию . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю:

что и требовалось доказать.

43. Теорема Коши.

Пусть даны две функции и такие, что: и определены и непрерывны на отрезке ; производные 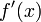и 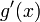конечны на интервале 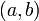; производные и не обращаются в нуль одновременно на интервале ; тогда 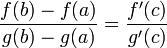, где (Если убрать условие 4, то необходимо усилить условие 3: g'(x) не должна обращаться в ноль нигде в интервале (a,b).)

Геометрически это можно переформулировать так: если f и g задают законы движения на плоскости (то есть определяют абсциссу и ординату через параметр t), то на любом отрезке такой кривой, заданном параметрами a и b, найдётся касательный вектор, коллинеарный вектору перемещения от (f(a);g(a)) до (f(b);g(b)).

Доказательство

Для доказательства введём функцию

Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а равна как раз необходимому числу.

44. Правило Лопиталя раскрытия неопределенности 0/0

Точная формулировка

Условия:

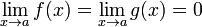1. или ;

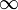2. и дифференцируемы в проколотой окрестности ;

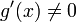3. в проколотой окрестности ;

4. существует ,

тогда существует .

Пределы также могут быть односторонними.

Отношение бесконечно малых

Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида ).

Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a, мы можем непрерывным образом их доопределить в этой точке: пусть f(a) = g(a) = 0. Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку теорему Коши. По этой теореме получим:

,

но f(a) = g(a) = 0, поэтому .

Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим:

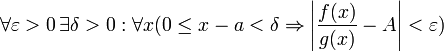для конечного предела и

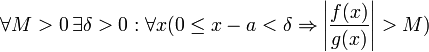для бесконечного,

что является определением предела отношения функций.

45. Правило Лопиталя для раскрытия неопределенности ∞/∞

Точная формулировка

Условия:

1. или ;

2. и дифференцируемы в проколотой окрестности ;

3. в проколотой окрестности ;

4. существует ,

тогда существует .

Пределы также могут быть односторонними.

Отношение бесконечно больших

Докажем теорему для неопределённостей вида .

Пусть, для начала, предел отношения производных конечен и равен A. Тогда, при стремлении x к a справа, это отношение можно записать как A + α, где α — O(1). Запишем это условие:

.

Зафиксируем t из отрезка и применим теорему Коши ко всем x из отрезка :

, что можно привести к следующему виду:

.

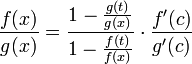Для x, достаточно близких к a, выражение имеет смысл; предел первого множителя правой части равен единице (так как f(t) и g(t) — константы, а f(x) и g(x) стремятся к бесконечности). Значит, этот множитель равен 1 + β, где β — бесконечно малая функция при стремлении x к a справа. Выпишем определение этого факта, используя то же значение ε, что и в определении для α:

.

Получили, что отношение функций представимо в виде (1 + β)(A + α), и 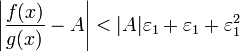. По любому данному ε можно найти такое ε₁, чтобы модуль разности отношения функций и A был меньше ε, значит, предел отношения функций действительно равен A.

Если же предел A бесконечен (допустим, он равен плюс бесконечности), то

.

В определении β будем брать ; первый множитель правой части будет больше 1/2 при x, достаточно близких к a, а тогда .

46. Локальная формула Тейлора. Остаточный член в форме Пеано.

Пусть  -- остаток в формуле Тейлора для функции в точке , и функция имеет непрерывную -ю производную. Тогда  -- бесконечно малая величина того же или большего порядка малости, как , при . (Остаточный член , о котором известны эти сведения о порядке малости, называется остаточным членом в форме Пеано.)

Остаточный член в форме Пеано: В форме Пеано:

при

   Доказательство.     Утверждение теоремы означает, что существует

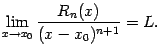
При остаток будет иметь тот же порядок малости, что , а при  -- больший порядок малости. Итак, вычислим предел:

Применим к этому пределу правило Лопиталя, повторив этот приём раз:

47. Формула Тейлора с остаточным членом в форме Лагранжа и Коши.

Теорема 6.2 (остаток в формуле Тейлора в форме Лагранжа)   Пусть при всех существует -я производная . Тогда для любого существует точка , лежащая между и (то есть при ), такая что

(Остаточный член формулы Тейлора, представленный в таком виде, называется остаточным членом в форме Лагранжа.)

        Доказательство.     Это доказательство не столь прямолинейное, как в предыдущей теореме. Рассмотрим вспомогательную функцию переменного , изменяющегося в рассматриваемой окрестности точки . Эта функция будет зависеть также от параметра :

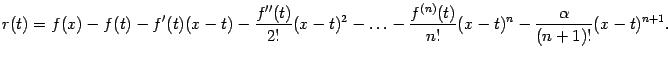
Подберём такое значение параметра , равное , чтобы при функция обращалась в 0: . Фиксируем такое значение .

Тогда функция удовлетворяет условиям теоремы Ролля на отрезке (или , если ): , что очевидно по определению функции ; согласно выбору параметра; дифференцируемость на и непрерывность в точках и следуют из предположенных свойств функции . По теореме Ролля существует такая точка , что

Однако нетрудно подсчитать, находя производные произведений в определении функции , что

Все слагаемые в начале правой части, включая обозначенные многоточием, взаимно уничтожаются, так что получаем

Подстановка даёт

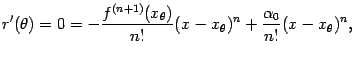
откуда следует, что

Теперь вспомним, что значение параметра мы выбрали так, что . Подставив найденное значение в выражение для , получим:

Отсюда получаем, наконец,

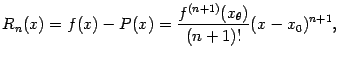
что и требовалось доказать.     

48. Основные разложения по формуле Тейлора.

Разложение основных элементарных функций - Положив и вычислив соответствующие производные в нуле, получим формулы Тейлора для основных элементарных функций:

• ; 

• ;

• ;

• ;

• ; 

• ;

• .

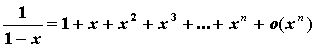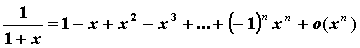49. Условия монотонности функции.

50. Экстремум функции. Необходимое условие экстремума.

Пусть дана функция и  — внутренняя точка области определения f. Тогда

• x₀ называется точкой локального максимума функции f, если существует проколотая окрестность такая, что

• x₀ называется точкой локального минимума функции f, если существует проколотая окрестность такая, что

Если неравенства выше строгие, то x₀ называется точкой строгого локального максимума или минимума соответственно.

• x₀ называется точкой абсолютного (глобального) максимума, если

• x₀ называется точкой абсолютного минимума, если

Значение функции f(x₀) называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.

Следующая теорема даёт необходимое условие того, чтобы точка была точкой локального экстремума функции .

        Теорема 7.4   Если точка  -- это точка локального экстремума функции , определенной в некоторой окрестности точки х0, и существует производная в этой точке , то .

Доказательство этой теоремы сразу же следует из теоремы Ферма (см. гл. 5).    

Утверждение теоремы можно переформулировать так:

если функция имеет локальный экстремум в точке , то либо 1) , либо 2) производная не существует.

Точка называется критической точкой функции , если непрерывна в этой точке и либо , либо не существует. В первом случае (то есть при ) точка называется также стационарной точкой функции .

Итак, локальный экстремум функции может наблюдаться лишь в одной из критических точек этой функции.

51. Достаточное условие экстремума, использующее первую производную.

Пусть в точке  функция  непрерывна, а производная  при переходе через точку  меняет знак. Тогда  – точка экстремума: максимума, если знак меняется с «+» на «–», и минимума, если с «–» на «+».

Доказательство. Пусть  при  и  при .

По теореме Лагранжа , где .Тогда если , то ; поэтому  и , следовательно, , или . Если же , то ; поэтому  и , следовательно,  или .

Таким образом доказано, что  в любых точках вблизи , т.е.  – точка максимума функции .

Доказательство теоремы для точки минимума проводится аналогично. Теорема доказана.

Если при переходе через точку  производная не меняет знак, то в точке  экстремума нет.

52. Достаточное условие экстремума, использующее высшие производные.

Пусть  -- стационарная точка функции , и в этой точке существует вторая производная , причём . Тогда при точка есть точка локального максимума, а при  -- локального минимума.

        Доказательство.     Поскольку , то по определению производной

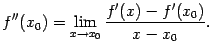
Пусть . Тогда из существования предела следует, что для любого из некоторой достаточно малой проколотой окрестности точки выполняется то же неравенство для допредельного выражения, то есть

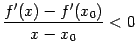
при . Поскольку, по предположению теоремы,  -- стационарная точка, то , откуда 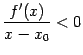, то есть имеет знак, противоположный знаку : при и при . Остаётся лишь применить теперь предыдущую теорему, из которой следует, что  -- точка локального максимума.

Доказательство для случая совершенно аналогично.     

53. Условия выпуклости и наличия точки перегиба графика функции.

Точка перегиба функции внутренняя точка x₀ области определения f, такая что f непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и x₀ является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.

Необходимое условие существования точки перегиба: если функция f(x), дважды дифференцируемая в некоторой окрестности точки x₀, имеет в x₀ точку перегиба, то .

Первое достаточное условие существования точки перегиба: если функция f(x) в некоторой окрестности точки x k раз непрерывно дифференцируема, причем k нечётно и , и при , а , то функция f(x) имеет в x₀ точку перегиба.

Второе достаточное условие существования точки перегиба: Если в некоторой точке вторая производная функции равна нулю, а третья не равна нулю, то эта точка является точкой перегиба.

54. Вертикальные и наклонные асимптоты.

Асимптотой графика функции  называется прямая, обладающая тем свойством, что расстояние от точки  до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Прямая x = a называется вертикальной асимптотой графика функции f (x) при x → a, если выполнено хотя бы одно из условий

,

Прямая y = b называется горизонтальной асимптотой графика функции f (x) при x → +∞, если

Прямая y = kx + b, k ≠ 0 называется наклонной асимптотой графика функции f (x) при x → +∞, если Аналогично определяются горизонтальная и наклонная асимптоты при x → –∞.

Для того, чтобы прямая y = kx + b была асимптотой графика функции y = f (x) при x → +∞, необходимо и достаточно, чтобы существовали конечные пределы