МАТЕМАТИЧЕСКИЙ АНАЛИЗ ( 2 СЕМЕСТР )
1. Неопределенный интеграл, первообразная функции.
2. Основные свойства неопределенного интеграла.
3. Таблица основных интегралов.
4. Интегрирование методом замены переменной.
5. Интегралы от функций, содержащих квадратный трехчлен.
6. Метод интегрирования по частям.
7. Интегрирование рациональных дробей.
8. Разложение дроби на простейшие.
9. Интегралы от тригонометрических функций.
10. Интегрирование иррациональных функций.
11. Тригонометрические подстановки для иррациональных функций.
12. Интегрирование дифференциального бинома.
13. Интегралы, не берущиеся в конечном виде.
14. Задача о площади криволинейной трапеции. Понятие определенного интеграла.
15. Формула Ньютона-Лейбница.
16. Основные свойства определенного интеграла.
17. Теорема о среднем значении.
18. Интегрирование по частям в определенном интеграле.
19. Приложения определенного интеграла. Вычисление площадей плоских фигур.
20. Приложения определенного интеграла. Вычисление объемов тел вращения.
21. Приложения определенного интеграла. Вычисление длины дуги плоской кривой.
22. Приложения определенного интеграла. Вычисление площади поверхности тела вращения.
23.Оценка определенных интегралов.
24. Несобственные интегралы 1-го рада.
25. Эталонный интеграл 1-го рода.
26. Несобственные интегралы 2-го рада.
27. Эталонный интеграл 2-го рода.
28. Сравнение несобственных интегралов.
29. Понятие функции нескольких переменных. Область определения. Графики. Примеры.
30. Линии и поверхности уровня.
31. Предел функции нескольких переменных.
32. Частные производные. Полный дифференциал.
33. Производная по направлению.
34. Градиент.
35. Производные и дифференциалы высших порядков.
36. Экстремум функции нескольких переменных.
37. Наибольшее и наименьшее значении ФНП
38. Условный экстремум. Метод множителей Лагранжа.
39. Интегрирование функций нескольких переменных. Двойные интегралы.
40. Свойства двойного интеграла. Сведение двойного интеграла к повторному.
41. Вычисление двойного интеграла (прямоугольная и произвольная области).
42. Замена переменной в двойном интеграле. Переход к полярным координатам.
43. Приложения двойного интеграла. Объем тела. Площадь плоской фигуры.
44. Понятие комплексного числа.
45. Арифметические операции над комплексными числами.
46. Комплексная плоскость. Функция комплексного переменного.
47. Тригонометрическая форма комплексного числа.
48. Извлечение корней из комплексного числа.
1. Неопределенный интеграл, первообразная функции. Понятие неопределенного интеграла.
Рассмотрим
такую задачу: Пусть задано ускорение,
как функция от времени
.
Требуется найти скорость и пройденный
путь в зависимости от времени.
Определение1.
Функция
на заданном промежутке называется
первообразной для функции
,
если во всем промежутке
является производной для
,
т.е.
есть дифференциал функции
.
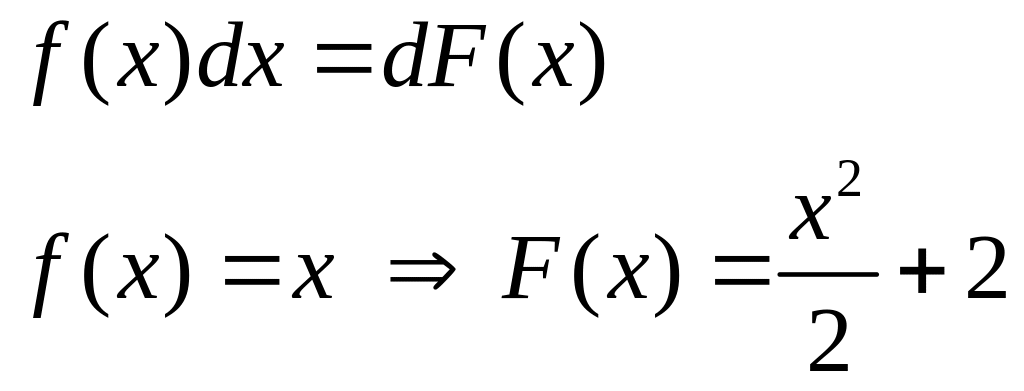
Разыскание для функции всех её первообразных, называемое интегрированием, составляет одну из задач интегрального исчисления.
Определение2.
Если
существует первообразная для функции
на промежутке
,
то множество первообразных на
называется неопределенным интегралом
от
и обозначается
.
Теорема 1.
Если
первообразная для
на промежутке
,
то выражение
(где
)
дает множество всех первообразных для
функции
на промежутке
.
Отсюда следует, что
2. Основные свойства неопределенного интеграла.
Непосредственно из определения интеграла вытекает следующие свойства:
Свойство1.
Свойство2.
Свойство3.
При
существовании конечной производной
справедливо следующее:
Свойство4.
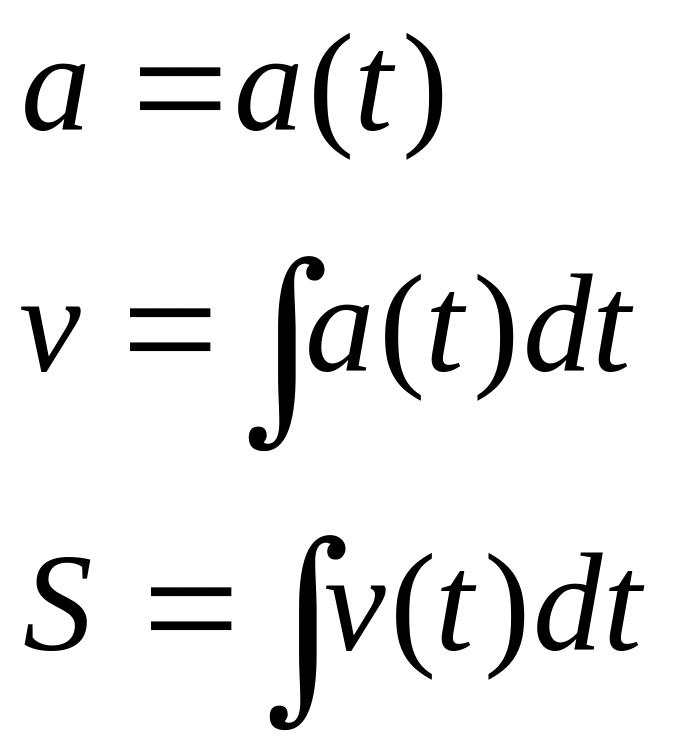
Пусть
Пусть
при
Известно,
что производная функции
дает угловой коэффициент касательной
к соответствующему графику. Поэтому
задача разыскания первообразной
для
можно истолковать так: требуется найти
кривую
,
для которой имел бы место заданный закон
изменения углового коэффициента
касательной
.
3. Таблица основных интегралов.
Всякая
формула для вычисления производной
автоматически выводит формулу для
вычисления первообразной. Поэтому из
таблицы производных перейдем к таблице
первообразных.
1)
2)
Отдельно
рассмотрим случай, когда
.
Так как
Более
того эта формула справедлива и для
3)
4)
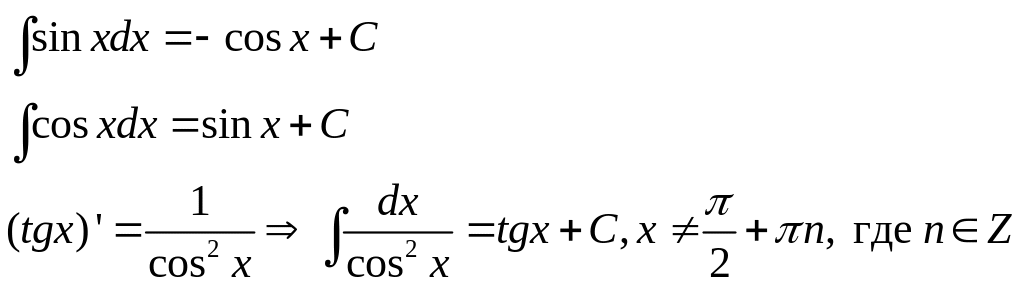
5)
6)
4. Интегрирование методом замены переменной.
Замена переменной в неопределенном интеграле (н.и.)
Теорема 1 (первый вариант замены переменной)
Пусть
надо вычислить н.и.
.
Если функция
дифференцируема на
и
интеграл
на промежутке
,
тогда (1)
на
.
Формулу (1) часто записывают в виде:
(1)’
После
вычисления интеграла справа, вместо t
подставим
.
Формулы
(1) и (1)’ получаются, если бы мы ввели
вместо
переменную
t,
.
Пример:
1)
2)
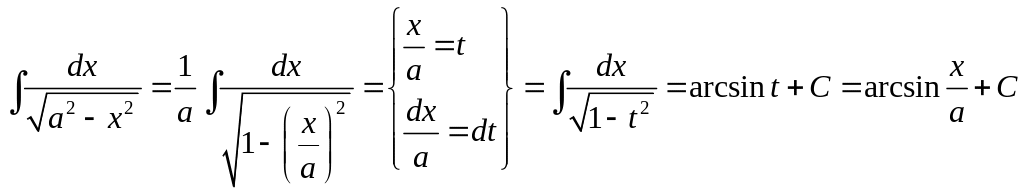
3)
Теорема 2 (второй вариант замены переменной)
Пусть
надо вычислить интеграл
.
Если некоторая функция
дифференцируема на
и
на
,
то (2)
В
формуле (2) мы формально вводим новую
функцию
.
5. Интегралы от функций, содержащих квадратный трехчлен.
I.
Рассмотрим интеграл
.
Преобразуем предварительно трехчлен,
стоящий в знаменателе, представив его
в виде суммы или разности квадратов.
где
обозначено
.
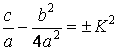Знак
плюс или минус берется в зависимости
от того, будет ли выражение, стоящее
слева положительным или отрицательным,
т. е. будут ли корни трехчлена
действительными
или комплексными. Таким образом, интеграл
принимает
вид
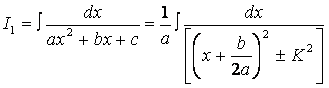
Сделаем
замену
,
dx=dt
тогда получим
Если в последней формуле получается плюс, то
1°)
вычисляется по формуле
,
который мы с Вами вывели. Т. е. получаем
2°) Если в формуле получаем (-), то
вычисляется по следующей формуле
,
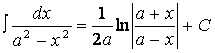(20º)
которую, мы обоснуем позже. Тогда в нашем случае:
=
.
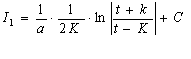6. Метод интегрирования по частям.
Интегрирование по частям.
Всякое
подынтегральное выражение можно
различными способами представить в
виде
,
где
-
функции переменной интегрирования
Интегрирование
по частям называется сведение данного
интеграла к интегралу
с помощью определения формулы.