
- •Модуль 1. Числовые и линейные неравенства
- •Практическая часть
- •Устные упражнения
- •Практическая часть
- •Устные упражнения
- •Входная информация
- •Практическая часть
- •«Линейное неравенство с одной переменной»
- •Практическая часть
- •Устные упражнения
- •Линейных неравенств
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •10 Класс.
- •Рубрика «Ваш помощник»
- •Сводящихся к линейным неравенствам
- •Входная информация
- •1) Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится неравенство, равносильное исходному;
- •2) Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится неравенство, равносильное исходному;
- •3) Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное исходному.
- •Практическая часть
- •Устные упражнения
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •Краткие исторические сведения о неравенствах
- •Интересно знать
- •Кто сильнее?
- •Практическая часть
- •Устные упражнения
- •Рубрика “Ваш помошник”
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Практическая часть
- •5) Найденные множества решений объединяют и записывают ответ.
- •Практическая часть
- •Входная информация
- •Практическая часть
- •Рубрика “Ваш помощник”
- •Входная информация.
- •Рубрика “Ваш помощник”
- •Краткие исторические сведения о неравенствах
- •Интересно знать
- •Кто сильнее?
- •Нематематики о математике
- •Практическая часть
- •Содержащих квадратные корни
- •Входная информация
- •Практическая часть
- •Входная информация
- •Входная информация
- •Математическая мозаика Из истории введения действия извлечения квадратного корня из числа
- •Интересные задачи
- •Софизмы
- •А. Эйнштейн
- •Модуль 4.
- •Квадратные уравнения.
- •Уравнения, сводящиеся к квадратным уравнениям
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •Рубрика «Ваш помощник»
- •Входная информация
- •Рубрика «Ваш помощник»
- •На линейные множители
- •Входная информация
- •Упражнения
- •Рубрика «Ваш помощник»
- •Уэ 5. Теорема Виета
- •Входная информация
- •Рубрика «Ваш помщник»
- •Входная информация
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •Рубрика «Ваш помощник»
- •Входная информация
- •С целыми коэффициентами
- •Практическая часть
- •Учимся доказывать теоремы
- •Содержание
Сводящихся к линейным неравенствам
Ваша цель: знать и уметь применять утверждения, на основе которых осуществляются равносильные переходы; научиться решать неравенства, сводящиеся к линейным.
Входная информация
Основная идея решения неравенства. Она заключается в следующем: заменяем одно неравенство другим, более простым, но равносильным первому. Такие замены осуществляются на основе следующих утверждений:
1) Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится неравенство, равносильное исходному;
2) Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится неравенство, равносильное исходному;
3) Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное исходному.
Например, неравенство
–12 + 3х > 0 (1)
равносильно неравенству
3х > 12, (2)
а неравенство 3х > 12 равносильно неравенству х > 4.
Учимся решать неравенства. Рассмотрим примеры решения неравенств, сводящихся к линейным неравенствам.
Пример 1. Решим неравенство 3x + 9 > 0.
Решение. Перенесем слагаемое 9 с противоположным знаком в левую часть неравенства: 3x > –9.
Разделив обе части неравенства на положительное число 3, получим равносильное ему неравенство x > –3.
Множество решений неравенства состоит из всех действительных чисел больше –3. Это множество представляет собой числовой промежуток (–3; +¥), изображенный на рисунке 1.
Ответ можно записать в виде числового промежутка (–3; +¥).
Ответ: (– 3; +¥).
Пример 2. Решим неравенство
– 2 ³ – 7.
Умножив обе части неравенства на 15, получим равносильное ему неравенство: 5х – 30 ³ 6x – 105.
Перенеся члены неравенства из одной части в другую с противоположным знаком, придем к неравенству 5x – 6x > 30 – 105. Откуда –x > –75.
Умножим обе части неравенства на –1, поменяв знак неравенства на противоположный: х £ 75.
Ответ: (–¥; 75].
Практическая часть
Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы на все устные упражнения приведенные ниже. Затем свои ответы сверьте с ответами или краткими указания, помещенными в конце этого учебного элемента в рубрике «Ваш помощник».
Устные упражнения
Решите неравенство:
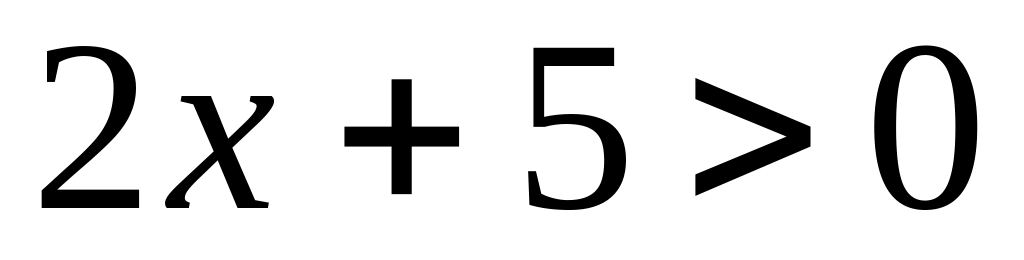 ;
;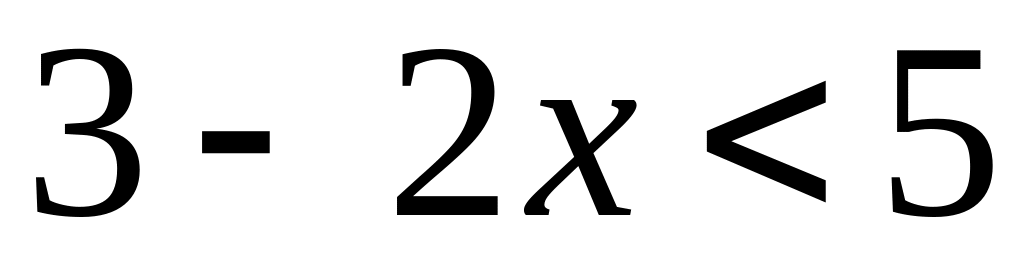 ;
;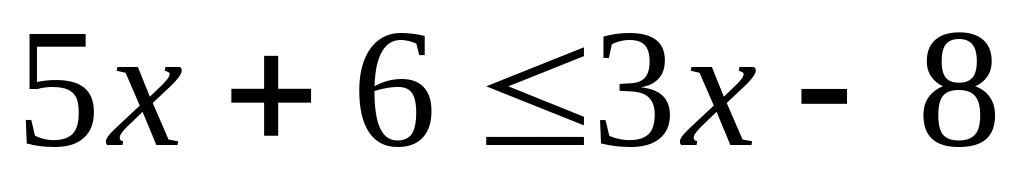 ;
;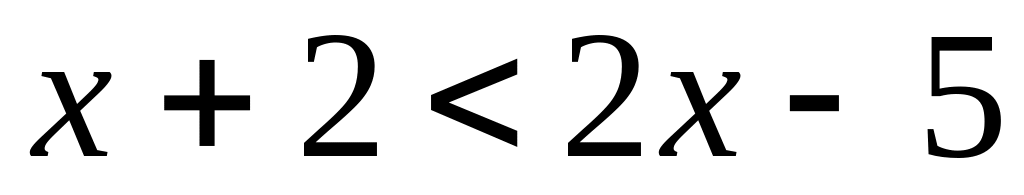 .
.
Найдите область определения выражения:
;
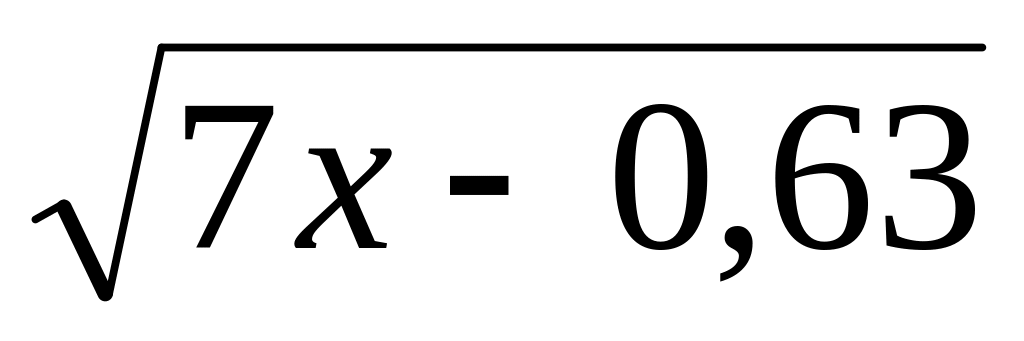 ;
;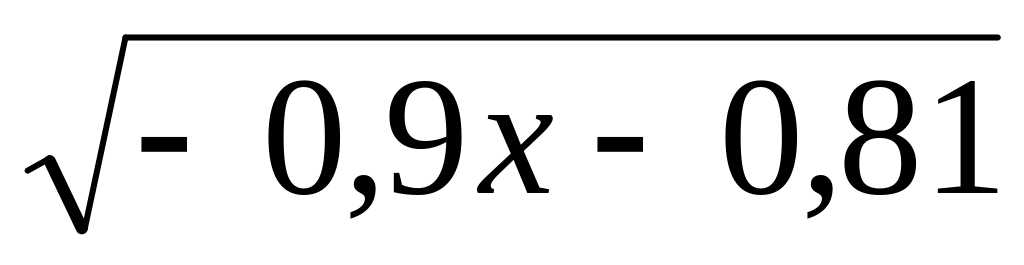 ;
;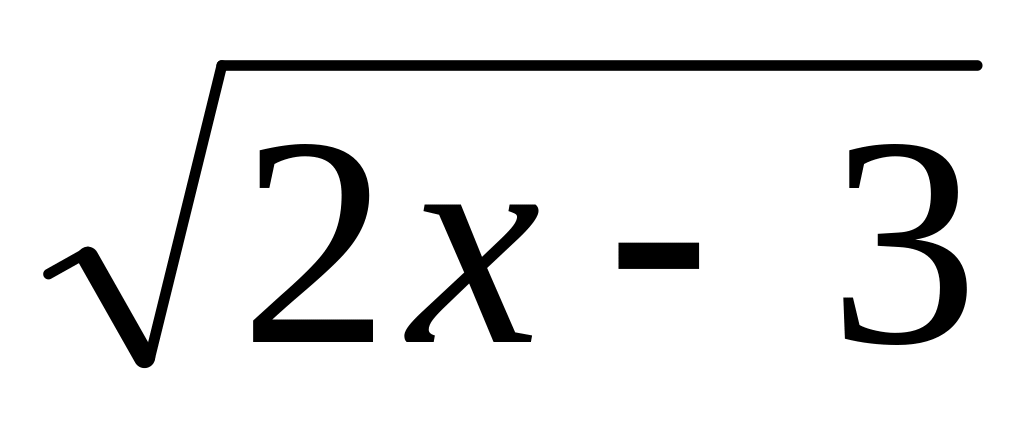 .
.Найдите область определения выражения:
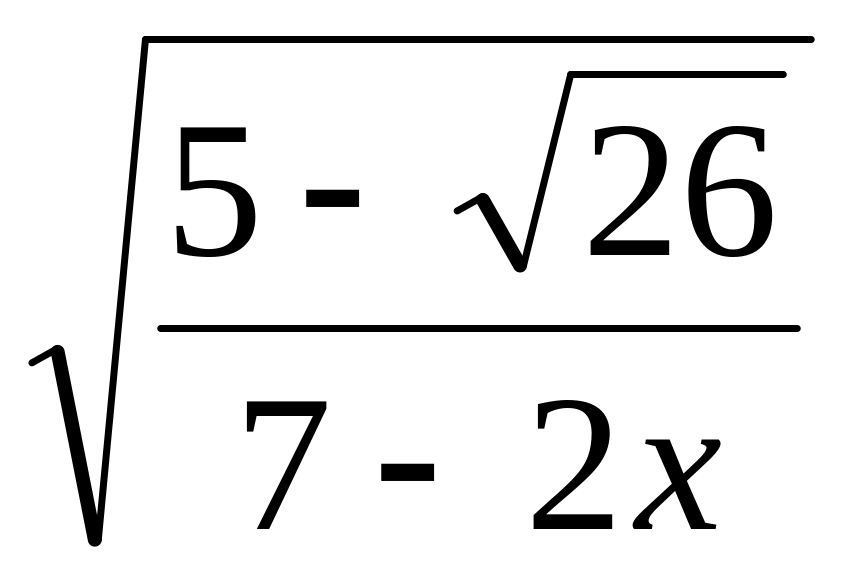 ;
;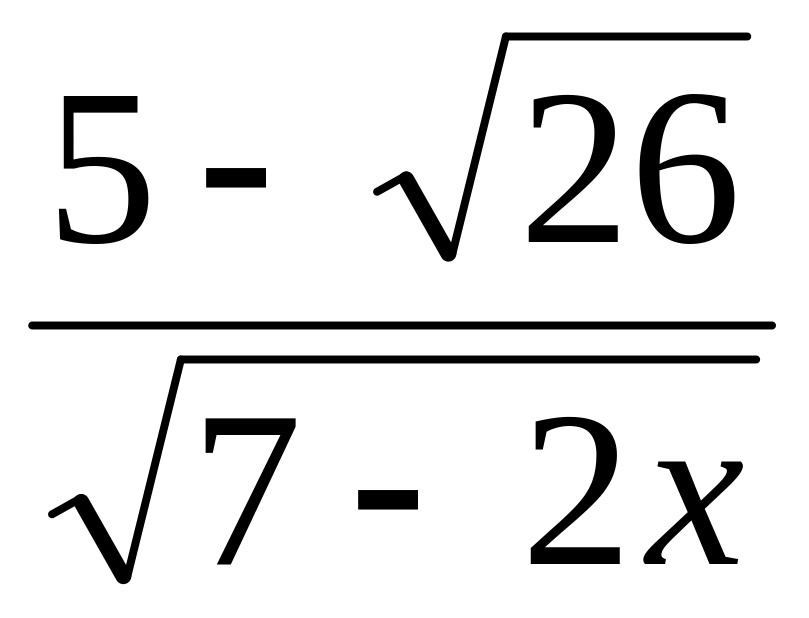 .
.
С некоторыми видами из следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из заданий вам необходимо выполнить. В случае трудностей обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу.
Задание 2. Решите неравенство:
а) (3x + l)(x – l) – 3x2 > 5 – 2x;
б) (2x – 5)2 – l < (2b –l)(2b + l) –15;
в) 3c2 – (3c +2)(c – l) > 8;
г) (3k – 2)(2k + 3) –(6k2 – 85) ³ 99.
Задание 3. Решите неравенство:
а) (x + 1)(x + 2) – (х –3)(х + 4) < 6;
б) 3(t + l)(t + 2) – (3t – 4)(t + 2) ³ 35;
в) 2(3а – 1)(2а + 5) – 6(2а – 1)(а + 2) < 48;
г) 3(1 – 4x)(x – 1) + 2(6х – 4)(x + 3) > 59.
Задание 4. Решите неравенство:
a) – < ;
б) (0,4x – 2) – (1,5x + 1) ³ 3,6 + (–4x – 0,8);
в) (l – 2a) + (–l,6a – l) £ 5,4 + (–2,5 – 0,3a);
г) (0,15b – ) + (2,3b – 0,25) > 3,12 + (2 – 0,25b).
Задание 5. Решите неравенство:
а) (2x – l)2 +5x < (l + 2x)(2x – l);
б) (x – 1)2 – (1 +x)(1 –x) < 2(l –x)2;
в) (y – 1)2 – 2(4 + y)(y – 1) +(y + 4)2 > 5y;
г) (2y – l)3 – (2y + 3)
Задание 6.Решите неравенство:
а) – ; г) < ;
б) + 1 > – ; д) – > ;
в) – > 1; е) – < 1 – .
Задание 7. Решите неравенство:
а) 3(2x – 1) – < – 7;
б) – < + 3;
в) 3 + > – ;
г) < 5.
Задание 8. Найдите область определения функции, заданной формулой:
а) y = ; в) y = ;
б) y = ; г) y = –.
Задание 9. При каких действительных значениях переменной х имеет смысл выражение:
а) ; в) ;
б) ; г) ;
д) .
Задание 10. Найдите все значения x Î N и удовлетворяющие неравенству:
а) 7х – 6 < 4х + 9;
б) (2 – 1,2х) – (0,5х – 6,5) > 0;
в) –27,1 +3x < 7,1 – 5x.
Задание 11..Найдите наибольшее целое решение неравенства:
– < 1 – .
Задание 12. Длина стороны прямоугольника равна 12 дм. Какой должна быть длина другой стороны, чтобы численное значение периметра прямоугольника было меньше численного значения периметра квадрата со стороной 9 дм?
Задание 13. Длина стороны прямоугольника равна 12 см. Какой должна быть длина другой стороны, чтобы численное значение периметра прямоугольника было больше численного значения площади этого прямоугольника?
Задание 14. Туристы отправились на моторной лодке по течению реки и должны вернуться обратно к стоянке не позднее чем через 3 ч.
На какое расстояние могут отъехать туристы, если скорость течения реки 2 км/ч, а скорость лодки в стоячей воде 18 км/ч?
Задание 15. Из города A со скоростью 12 км/ч выехал велосипедист. Через t ч вслед за ним из того же города отправляется мотоциклист со скоростью 30 км/ч.
Найдите те значения t, при которых мотоциклисту понадобится менее 4 ч для того, чтобы догнать велосипедиста.
