Практическая часть
Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы на все устные упражнения приведенные ниже. Затем свои ответы сверьте с ответами или краткими указания, помещенными в конце этого учебного элемента в рубрике «Ваш помощник».
Устные упражнения
1. Решите неравенство:
а) 2х > 7; в) 2х < –3; д) 8у > 0; ж) (а2 + 1)х > –1;
б) –2х > 8; г) –0,4х < 6; е) –8у > 0; з) –(b2 + 1)у < 0.
2. Решите неравенство
а) 0х > 7; г) 0х < 7; ж) 0х > –7;
б) 0х > 13,5; д) 0х < 13,5; з) 0х < –7;
в) 0х > 0; е) 0х < 0; и) 0х £ –7.
3. Решите неравенство ax > 5, если:
а) a < 0; б) a = 0; в) a > 0.
4. Решите неравенство ax > b, если:
а) a > 0; б) a < 0; в) a = 0, b > 0; г) a = 0, b < 0.
5. Решите неравенство ax < b, если:
а) a > 0; б) a < 0; в) a = 0, b > 0; г) a = 0, b < 0.
6. Решите неравенство:
а) 0 · х < 3; г) 0 · х > –2а2 – 1; ж) 0 · х < а2 – 2a + 1;
б) 0 · х < 5а2 + 1; д) 0 · х > 0; з) 0 · х ³ 1 – 2a + а2;
в) 0 · х > – a; е) 0 · х < 2a – 3; и) 0 · х ³ 1 –а2.
7. При каких значениях a одновременно имеют место неравенства:
а) aх – 5 > 0 и х > ; в) 3х – a > 0 и ;
б) aх – 5 > 0 и х < ; г) 7a + 9 < 0 и х < –?
8. Можно ли утверждать, что при любом действительном a:
а) ïaï ³ a; б) 2a > a; в) a + 1 >a –1 ?
Задание 2. Решите относительно х неравенство:
а) ax > –7; д) (a – 4) < x < b – 1;
б) (a – 3)x > 2; е) (2a + 1)x > 2b – 7;
в) (2a – 1)x < 4; ж) (a – 1)x > 5a + 1;
г) ax < b; з) a(x – 1) > x – 2.
10 Класс.
Задание
3. Решите относительно переменной
неравенство:
а)
е)
б)
ж)
в)
з)
г)
и)
д)
к)
Задание 4. Решите относительно переменной неравенство:
а)
г)
б)
д)
в)
е)
ж)
з)
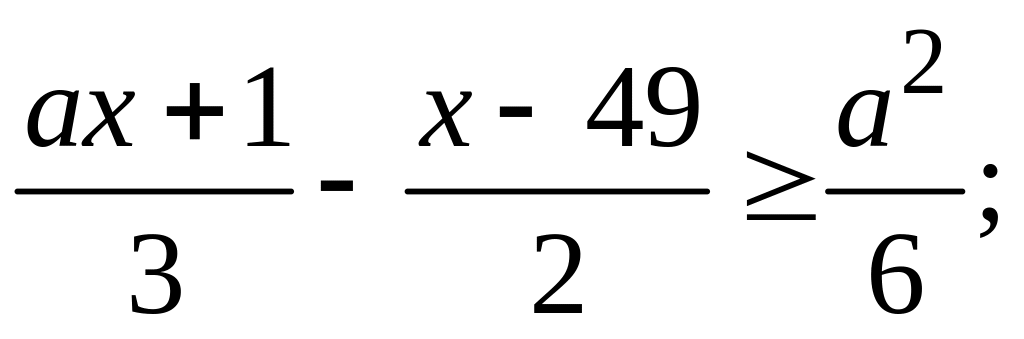
и)
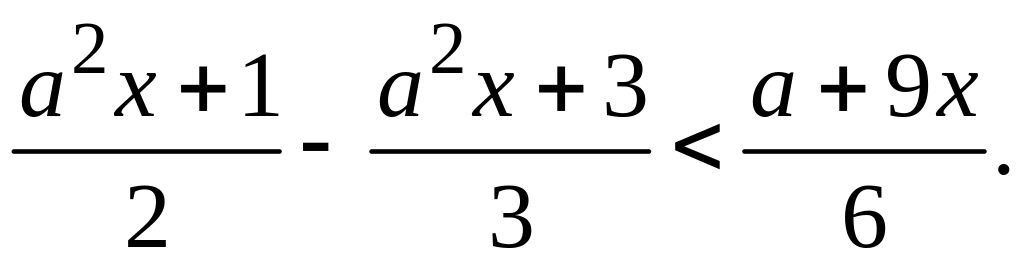
Рубрика «Ваш помощник»
К заданию 1. Ответы или краткие указания:
1. а) (3,5; +¥); б) (–¥; –4); в) (–¥; –1,5); г) (–15; +¥);
д) (0; +¥); е) (–¥; 0); ж) (–; +¥); з) (0; +¥).
2. а) Æ; б) Æ; в) Æ; г) R; д) R; е) R; ж) R; з) Æ; и) Æ.
3. а) так как a < 0, то (ax > 5) Û (х < ), т.е. (–¥; );
б) так как а = 0, то неравенство имеет вид 0 × 5 > 5; множество его решений – пустое;
в) так как а > 0, то (ax > 5) Û (х > ), т.е. (; +¥).
4. а) так как а > 0, то (ax > b) Û (х > ). Его решение – числовой промежуток (; +¥);
б) так как a < 0, то (ax > b) Û (х < ). Его решение – числовой промежуток (–¥;);
в) В этом случае неравенство имеет вид 0 × х > b, а так как b > 0, то множество решений данного неравенства – пустое;
г) в этом случае неравенство имеет вид 0 × х > b, а так как b < 0, то его решением является любое действительное число, т.е. множество R.
5. а) (–¥; ); б) (; +¥); в) R; г) Æ.
6. а) R; б) R; в) если a > 0, то множество R; если a < 0, то Æ; г) R; д) Æ; е) если a > , то решением является множество R; если a £ , то Æ; ж) если a = 1, то решением является Æ; если a ¹ 1, то R; з) если a = 1, то решением является множество R; если a ¹ 1, то Æ; и) если ïхï£, то решением является множество R; если ïаï > 1, то Æ.
7. а) при a > 0; б) при a < 0; в)
8. а) да; б) нет; в) да.
УЭ-6. Решение неравенств,