Рубрика «Ваш помощник»

К заданию 1. Ответы к устным упражнениям.

1. а) х(х – 3) = 70. Искомые числа: 10 и 7 либо –10 и –7;

б) х(х + 3) = 10. Катеты треугольника: 2 5 см. Учащимся можно предложить угадать корни составленных уравнений.

2. а) х² – (х – 9)² = 279, где х – большее число;

б) х² = (х – 8)² + (х – 4)²; в) n² + (n + 1)² + (n + 2)² = 1589.

Уэ 5. Теорема Виета

Ваша цель: знать теорему Виета для квадратного уравнения и уметь применять ее для решения разнообразных задач.

Входная информация

Для квадратного уравнения теоремы Виета формулируется так.

Теорема 1. Если квадратное уравнение имеет действительные корни и , то их сумма равна , а произведение равно .

Теорема 1. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а их произведение равно свободному члену.

В частности, сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а их произведение равно свободному члену.

Теорема 2. Если числа и таковы, что их сумма равна , а произведение , то эти числа являются корнями уравнения .

В частности, если , то числа и являются корнями приведенного квадратного уравнения .

Как уже отмечалось, используя теорему, обратную теореме Виета, можно находить корни приведенного квадратного уравнения путем подбора.

Если заданы корни квадратного уравнения, то можно составить и само уравнение, используя теорему, обратную теореме Виета. Рассмотрим это на примерах.

Пример 1. Составим квадратное уравнение, корни которого равны: .

Решение. Найдем сумму и произведение корней: . Искомое уравнение: .

Пример 2. Составим квадратное уравнение, корни которого равны .

Решение. Найдем сумму и произведение корней: . Искомое уравнение: , или .

Практическая часть

Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже.

Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник».

Устные упражнения

1. Не решая уравнения, укажите сумму и произведения корней уравнения. Подберите корни уравнения:

а) х² – 13х + 12 = 0; в) х² – 7х + 10 = 0;

б) х² –х – 2 = 0; г) х² – 3х – 10 = 0.

2. Составьте приведенное квадратное уравнение, зная его корни:

а) 2 и 7; б) –7 и 3; в) –10 и –30; г) 0 и 7.

3. Составьте квадратное уравнение, имеющее: а) два положительных корня; б) два отрицательных корня.

4. При каком условии по крайней мере один из корней уравнения ах² + bх + с = 0 равен 0 ?

5. При каком значении а равенство является тождеством:

а) х² + 5х + а = (х + 2)(х + 3); б) х² + ах + 2 = (х + 1)(х + 2) ?

6. Зная, что данное равенство является тождеством, найдите а и k:

а) х² – 9х – 22 = (х + а)(х – 2); б) 3х² + 17х – 6 = (kх + а)(х + 6).

7. Почему квадратное уравнение с рациональными коэффициентами не может иметь один корень рациональный, а другой – иррациональный ?

8. Не решая уравнения х² – 2х – 1 = 0, определите, является ли число 1 – его корнем.

9. Почему приведенное квадратное уравнение с иррациональными коэффициентами не может иметь двух рациональных корней ?

10. Корень квадратного уравнения с рациональными коэффициентами:

а) х₁ = 1 – ; б) х₁ = 2 + .

Укажите второй корень и соответствующее уравнение.

11. Корни какого из уравнений х² – 7х = 0, х² – 2х – 24 = 0, х² – 12х + 36 = 0, х² – 2х + 24 = 0, х² – 7х – 14 = 0 обладают свойством:

а) сумма корней равна 7, а произведение корней равно – 14;

б) один из корней равен 7;

в) корни равны.

12. Определите недостающие коэффициенты в следующих квадратных уравнениях:

а) х² – 6х + … = 0, если х₁ = 2, х₂ = …;

б) х² – …х + 18 = 0, если х₁ = 3, х₂ = …;

в) х² – 5х + … = 0, если х₁ = –1, х₂ = … .

С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу.

Задание 2. Решите уравнение и выполните проверку по теореме, обратной теореме Виета:

а) ; г) ;

б) , д) ;

в) ; е) .

Задание 3. Найдите подбором корни уравнения:

а) ; д) ;

б) ; e) ;

в) ; ж) ;

г) ; з) .

Задание 4. Может ли уравнение , где р и q – рациональные числа, иметь корни:

а) ;

б) ;

в) ?

Задание 5. Почему квадратное уравнение с рациональными коэффициентами не может иметь один корень рациональный, а другой иррациональный ?

Задание 6. Составьте квадратное уравнение, имеющее корнями следующие числа:

а) 3 и 1,5; б) – 0,2 и – 0,2; в) + 2 и – 2; г) и ; д) и .

Задание 7. Составьте квадратное уравнение с рациональными коэффициентами, один из корней которого равен:

а) ; б) ; в) .

Задание 8. Составьте квадратное уравнение, корнями которого являются взаимно обратные числа а и .

Задание 9. Составьте квадратное уравнение, имеющее корень .

Задание 10. Составьте квадратное уравнение, корни которого были бы на 2 меньше корней уравнения .

Задание 11. Не решая уравнения , найдите: а) ; б) ; в) ( и – корни уравнения).

Задание 12. Не находя корней уравнения , вычислите:

а) ; в) ; д) ;

б) ; г) ; е)

( и – корни исходного уравнения).

Задание 13. Не решая уравнения , определите 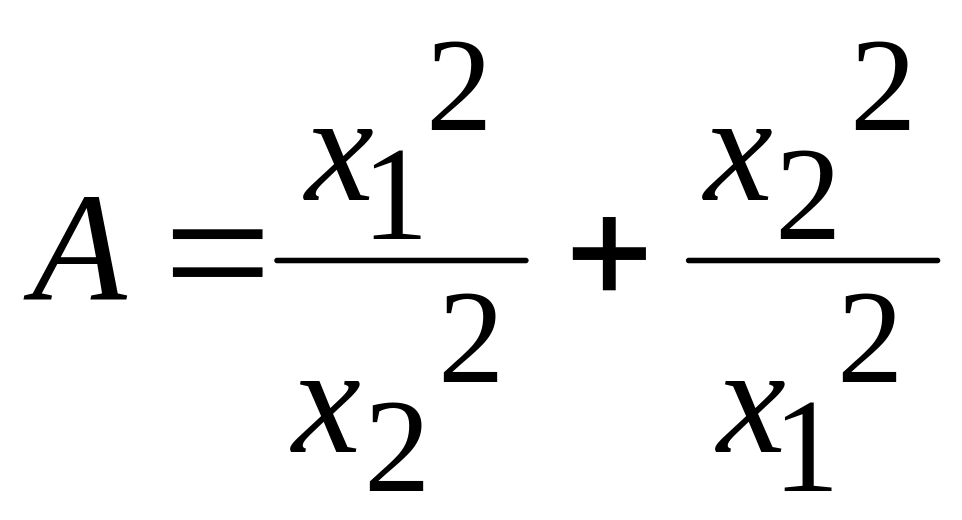, где и – корни исходного уравнения.

Задание 14. Не решая уравнения , найдите: а) ; б) , где и – корни этого уравнения.

Задание 15. Не решая уравнения , найдите , где и – корни этого уравнения.

Задание 16. Найдите все значения а, для которых квадрат разности корней уравнения равен 1.

Задание 17. Найдите зависимость между коэффициентами уравнения , если сумма кубов его корней равна произведению квадратов этих корней.

Задание 18. В каждом уравнении найдите р или q, использовав дополнительные условия:

а) , если ;

б) , если ;

в) , если ;

г) , если ;

д) , если .

Задание 19. В уравнении подберите значение k так, чтобы .

Задание 20. При каком значении q квадрат разности корней уравнения равен 16 ?

Задание 21. Какими должны быть р и q, чтобы уравнение имело корнями числа р и q ?

Задание 22. В уравнении найдите k, если