
- •Модуль 1. Числовые и линейные неравенства
- •Практическая часть
- •Устные упражнения
- •Практическая часть
- •Устные упражнения
- •Входная информация
- •Практическая часть
- •«Линейное неравенство с одной переменной»
- •Практическая часть
- •Устные упражнения
- •Линейных неравенств
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •10 Класс.
- •Рубрика «Ваш помощник»
- •Сводящихся к линейным неравенствам
- •Входная информация
- •1) Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится неравенство, равносильное исходному;
- •2) Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится неравенство, равносильное исходному;
- •3) Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное исходному.
- •Практическая часть
- •Устные упражнения
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •Краткие исторические сведения о неравенствах
- •Интересно знать
- •Кто сильнее?
- •Практическая часть
- •Устные упражнения
- •Рубрика “Ваш помошник”
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Входная информация
- •Практическая часть
- •Рубрика «Ваш помощник»
- •Практическая часть
- •5) Найденные множества решений объединяют и записывают ответ.
- •Практическая часть
- •Входная информация
- •Практическая часть
- •Рубрика “Ваш помощник”
- •Входная информация.
- •Рубрика “Ваш помощник”
- •Краткие исторические сведения о неравенствах
- •Интересно знать
- •Кто сильнее?
- •Нематематики о математике
- •Практическая часть
- •Содержащих квадратные корни
- •Входная информация
- •Практическая часть
- •Входная информация
- •Входная информация
- •Математическая мозаика Из истории введения действия извлечения квадратного корня из числа
- •Интересные задачи
- •Софизмы
- •А. Эйнштейн
- •Модуль 4.
- •Квадратные уравнения.
- •Уравнения, сводящиеся к квадратным уравнениям
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •Рубрика «Ваш помощник»
- •Входная информация
- •Рубрика «Ваш помощник»
- •На линейные множители
- •Входная информация
- •Упражнения
- •Рубрика «Ваш помощник»
- •Уэ 5. Теорема Виета
- •Входная информация
- •Рубрика «Ваш помщник»
- •Входная информация
- •Входная информация
- •Практическая часть
- •Устные упражнения
- •Рубрика «Ваш помощник»
- •Входная информация
- •С целыми коэффициентами
- •Практическая часть
- •Учимся доказывать теоремы
- •Содержание
Входная информация
Учимся решать задачи.
Пример 1. Упростим сумму
![]() .
.
Вынесем из-под
знака корня в выражении
![]() множитель
множитель
![]() ,
а в выражении
множитель
.
Получим:
,
а в выражении
множитель
.
Получим:
![]()
![]() .
.
Пример 2. Преобразуем произведение
![]() .
.
Вынеся общий множитель (число 3) за скобки в первом множителе, получим:
![]()
![]() .
.
Пример 3. Сократим дробь
![]() .
.
Пользуясь равенством
![]() ,
которое выполняется при
,
любое неотрицательное число можно
представить в виде квадрата некоторого
числа, в частности
,
которое выполняется при
,
любое неотрицательное число можно
представить в виде квадрата некоторого
числа, в частности
![]() .
Значит, числитель данной дроби можно
представить в виде разности квадратов
двух выражений:
.
Значит, числитель данной дроби можно
представить в виде разности квадратов
двух выражений:
![]() .
.
С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из заданий вам необходимо выполнить. В случае трудностей обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу.
Задание 1. Упростите выражение:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
Задание 2. Выполните действия:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
Задание 3. Упростите выражение:
а)
![]() ,
если
,
если
![]() ;
;
б)
![]() ,
если
,
если
![]() .
.
Задание 4. Выполните действия:
а)
![]() ; д)
; д)
![]() ;
;
б)
![]() ; е)
; е)
![]() ;
;
в)
![]() ; ж)
; ж)
![]() ;
;
г)
![]() ; з)
; з)
![]() .
.
Задание 5.
Докажите, что значения выражений
![]() и
и
![]() –взаимно обратные числа.
–взаимно обратные числа.
Задание 6. Упростите:
а)
![]() ; б)
; б)
![]() .
.
Задание 7. Выполните деление:
а)
![]() ; в)
; в)
![]() ;
;
б)
![]() ; г)
; г)
![]() .
.
Задание 8. Разложите на множители:
а)
![]() ; г)
; г)
![]() ,
если
;
,
если
;
б)
![]() ; д)
; д)
![]() ,
если
,
если
![]() ;
;
в)
![]() ; е)
; е)
![]() ,
если
,
если
![]() ;
.
;
.
Задание 9. Сократите дробь:
а)
![]() ; в)
; в)
![]() ; д)
; д)
![]() ;
;
б)
![]() ; г)
; г)![]() ; е)
; е)
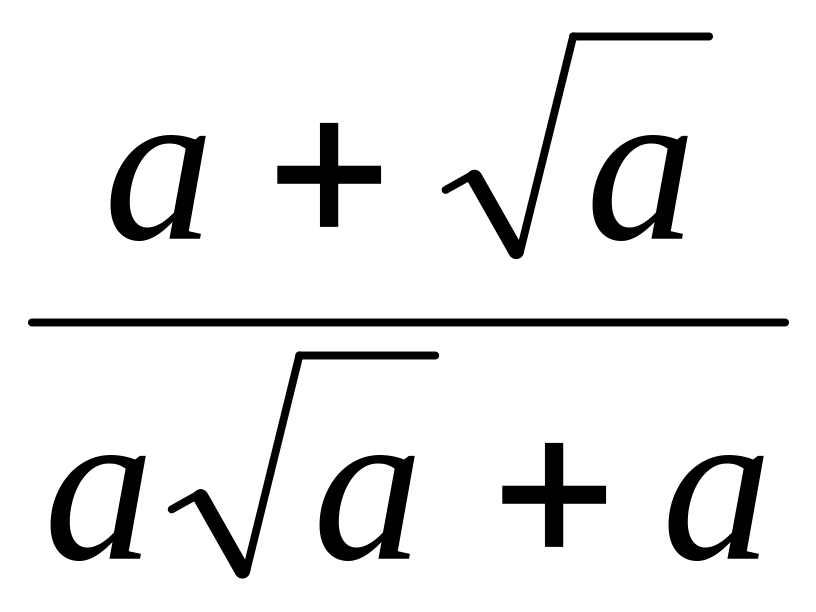 .
.
Задание 10. Упростите выражение:
а)
![]() ;
;
б)
![]() .
.
Задание 11. Докажите, что число а является корнем уравнения:
а)
![]() ;
;
б)
![]() .
.
Задание 12. Выполните действия:
а)
![]() ; в)
; в)
![]() ;
;
б)
![]() г)
г)
![]() .
.
Задание 13. Выполните действия:
а)
![]() ;
;
б)
![]() ;
;
в)
![]()
г)
![]() ;
;
д)
![]() ;
;
е)
![]() .
.
Рубрика «Ваш помощник»
К заданию 1. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
д)
;
д)![]() .
.
К заданию 2. Обозначив данное выражение через А, получим:
а)
![]() ;
;
б)
![]() ;
;
в)
![]()
![]()
г)
![]() ;
;
д)
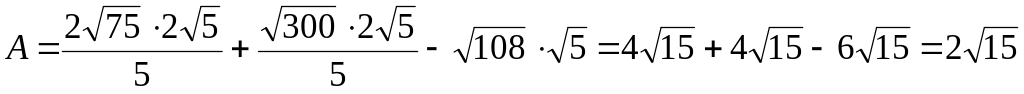 .
.
Ответы: а)
18; б)
![]() ;
в)
;
в)![]() ;
д) 2
;
д) 2![]() .
.
К заданию 3. а)
![]() ;
б)
;
б)
![]() .
.
К заданию 4. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
д) 10; е)
;
д) 10; е)![]() ;
з)
;
з)
![]() .
.
К заданию 5.
Имеем:
![]() .
.
К заданию 6. а) 25; б) 21.
К заданию 7. а)
8; б) 24; в)
![]() ;
г) 2.
;
г) 2.
К заданию 8. Обозначив данное выражение через А, получим:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() .
.
К заданию 10.
а)
![]() ;
б)
;
б)
![]()
УЭ-4. Преобразование двойных радикалов
Ваша цель: добиться того, чтобы ваши действия по преобразованию двойных радикалов удовлетворяли таким требованиям, как правильность, осознанность, рациональность и прочность.
Входная информация
Учимся решать задачи.
Выражение вида
![]() называют двойным, или сложным
радикалом.
называют двойным, или сложным
радикалом.
Если подкоренное выражение представляет собой полный квадрат, то можно в двойном радикале освободиться от внешнего радикала, воспользовавшись равенством
![]() .
.
Пример 1. Упростим выражение
![]() .
.
Слагаемое
можно рассматривать как удвоенное
произведение чисел 2 и
или 1 и
![]() .
Число 9 должно быть равно сумме квадратов
этих чисел. Очевидно, что это условие
выполняется для чисел 2 и
,
т.е.
.
Число 9 должно быть равно сумме квадратов
этих чисел. Очевидно, что это условие
выполняется для чисел 2 и
,
т.е.
![]() .
.
Тогда получим:
![]() .
.
Пример 2. Разность
![]()
является целым числом. Найдем это число.
Имеем:
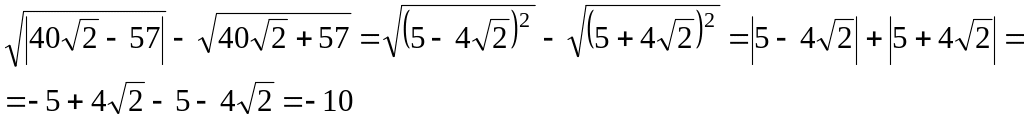 Итак,
на практике иногда удобно пользоваться
формулами:
Итак,
на практике иногда удобно пользоваться
формулами:
![]() ,
,
![]() ,
где
,
где
![]() .
.
В некоторых случаях при преобразованиях выражений, содержащих квадратные корни, полезно использовать тождество:
![]() ,
(1)
,
(1)
где
![]() ,
причем знаки берутся или только верхние,
или только нижние.
,
причем знаки берутся или только верхние,
или только нижние.
Это тождество иногда называют формулой сложного радикала.
Чтобы доказать равенство (1), заметим, что при левая и правая его части являются положительными числами.
Возведя левую
часть равенства (1) в квадрат, получим
![]() .
Возведя правую часть равенства (1) в
квадрат, получим:
.
Возведя правую часть равенства (1) в
квадрат, получим:
![]()
Итак, квадраты обеих частей равенства (1) равны, а так как эти числа положительные, то равенство (1) доказано.
Пример 3. Преобразуем выражение
![]() .
.
По формуле радикала имеем:
![]() С
некоторыми видами следующих заданий
вы могли встречаться на уроках математики.
Самоопределитесь, какие из заданий вам
необходимо выполнить. В случае трудностей
обращайтесь к рубрике «Ваш помощник»,
за консультацией к учителю или за помощью
к товарищу.
С
некоторыми видами следующих заданий
вы могли встречаться на уроках математики.
Самоопределитесь, какие из заданий вам
необходимо выполнить. В случае трудностей
обращайтесь к рубрике «Ваш помощник»,
за консультацией к учителю или за помощью
к товарищу.
Задание 1. Верно ли равенство:
а)
![]() ; б)
; б)
![]() ?
?
Ответ обоснуйте.
Задание 2.
Удовлетворяет ли число
![]() неравенству
неравенству
![]() ?
?
Задание 3. Освободитесь от внешнего радикала, представив подкоренное выражение в виде квадрата:
а)
![]() ; в)
; в)
![]() ; д)
; д)
![]() ;
;
б)
![]() ; г)
; г)
![]() ; е)
; е)
![]() .
.
Задание 4. Вычислите:
а)
![]() ; в)
; в)
![]() ;
;
б)
![]() ; г)
; г)
![]() .
.
Задание 5.
Разность
![]() является целым числом. Найдите это
число.
является целым числом. Найдите это
число.
Задание 6.
Разность
![]() является целым числом. Найдите это
число.
является целым числом. Найдите это
число.
Задание 7. Докажите, что значение выражения является целым числом:
а)
![]() ;
;
б)
![]() .
.
Задание 8. Упростите сложные радикалы:
а)
![]() ; в)
; в)
![]() ;
;
б)
![]() ; г)
; г)
![]() .
.
Задание 9. Докажите равенство:
а)
![]() ;
;
б)
![]() .
.
Задание 10.
Упростите выражение
![]() .
.
Задание 11. Докажите, что выражение
![]()
равно 2, если
![]() ;
равно
;
равно
![]() ,
если
,
если
![]() .
.
Задание 12.
Докажите, что
![]() .
.
Задание 13. Докажите, что
![]() .
.
Задание 14. Упростите выражение:
а)
![]() ; б)
; б)
![]() .
.
Рубрика «Ваш помощник»
К заданию 2. Да.
К заданию 3. а)
![]()
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
К заданию 4. а) 2; б) ; в) 2; г) 10.
К заданию 5. Имеем:
![]()
![]()
=![]() .
.
К заданию 6.
![]() .
.
К заданию 8. а)
![]() ;
в)
;
в)
![]() .
.
К заданию 11.
Преобразуем данное выражение, применив
формулу сложного радикала, или
воспользуемся методом подстановки:
![]() .
.
К заданию 12. Приведем знаменатели дробей к виду:
![]() ;
;
![]() .
.
Затем выполним преобразования, указанные в условии задачи.
К заданию 13.
Рассмотрим произведение двух последних
радикалов. Оно будет равно
![]() .
Произведение этого и второго радикала
будет равно
.
Произведение этого и второго радикала
будет равно
![]() .
Значит, все произведение будет равно
единице.
.
Значит, все произведение будет равно
единице.
