Входная информация
Понятие модуля
действительного числа.
Модулем
действительного числа
называют само это число
,
если
,
и противоположны ему число
,
если
< 0.
Модуль
числа
обозначают
и записывают:
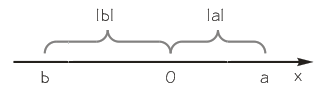
Геометрическая интерпретация модуля. Геометрически модуль действительного числа есть расстояние от точки, изображающей данное число на координатной прямой, до начала отсчета.
Решение
уравнений и неравенств с модулями на
основе геометрического смысла модуля.
Пользуясь понятием «расстояние между
двумя точками координатной прямой»
можно решать уравнения вида
или неравенства вида
,
где вместо знака
может стоять любой из знаков
.
Пример.
Решим уравнение
.
Решение.
Переформулируем задачу геометрически.
Поскольку
-это расстояние на координатной прямой
между точками с координатами
и
,
значит, требуется найти координаты
таких точек, расстояние от которых до
точек с координатой 1 равно 2.
Короче, на координатной прямой найти множество координат точек, расстояние от которых до точки с координатной 1 равно 2.
Решим эту задачу. Отметим на координатной прямой точку, координата которой равна 1 (рис. 6) На две единицы от этой точки удалены точки, координаты которых равны -1 и 3. Значит, искомое множество координат точек есть множество, состоящее из чисел -1 и 3.
Ответ: -1; 3.
Как найти
расстояние между двумя точками
координатной прямой. Число,
выражающее расстояние между точками
и
,
называют расстоянием между числами
и
.
Для любых двух точек и координатной прямой расстояние
.
Основные свойства модуля действительного числа:
1. 0;
2.
;
3.
;
4.
,
;
5.
;
6.
;
7.
;
8.
;
9.
;
10.
.
При
имеем:
11.
тогда только тогда, когда
или
;
12.
тогда только тогда, когда
;
13.
тогда только тогда, когда
или
;
14.
тогда только тогда, когда
;
11.
тогда только тогда, когда
.
Практическая часть
Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже.
Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник».
1. Раскройте знак модуля:
а) |–5|; б) |5|; в) |0|; г) |p|.
2. Сравните между собой числа:
а) || и –; в) |0| и 0; д) – |–3| и –3; ж) –4|а| и 0;
б) |–p| и p; г) |–7,3| и –7,3; е) |а| и 0; з) 2|а| и |2а|.
3. Как при помощи знака модуля записать, что по крайней мере одно из чисел а, b или с отлично от нуля ?
4. Как при помощи знака равенства записать, что каждое из чисел а, b и с равно нулю ?
5. Найдите значение выражения:
а) |а| – а; б) а + |а|.
6. Решите уравнение:
а) |х| = 3; в) |х| = –2; д) |2х – 5| = 0;
б) |х| = 0; г) |х – 3| = 4; е) |3х – 7| = – 9.
7. Что можно сказать о числах х и у, если:
а) |х| = х; б) |х| = –х; в) |х| = |у|?
8. Решите уравнение:
а) |х – 2| = х – 2; в) |х – 3| =|7 – х|;
б) |х – 2| = 2 – х; г) |х – 5| =|х – 6|.
9. Что можно сказать о числе у, если имеет место равенство:
а) ïхï = у; б) ïхï = –у ?
10. Решите неравенство:
а) |х| > х; в) |х| > –х; д) |х| £ х;
б) |х| ³ х; г) |х| ³ –х; е) |х| £ –х.
11. Укажите все значения а, для которых имеет место равенство:
а) |а| = а; б) |а| = –а; в) а – |–а| =0; г) |а|а = –1; д) = 1.
12. Найдите все значения b, для которых имеет место неравенство:
а) |b| ³ 1; б) |b| < 1; в) |b| £ 0; г) |b| ³ 0; д) 1 < |b| < 2.
С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу.
Задание 2. Исходя из определения модуля действительного числа, решите уравнение:
а) |x – 3| = 2; |
г) |3 – 2x| = 6; |
б) |4 – х| = 0,5; |
д) |2x – 5| = 0; |
в) 1– |х| = 0,5; |
е) |3х – 7| = – 9. |
Задание 3. Укажите на координатной прямой множество таких точек, для которых справедливо соотношение:
а) |x – 3| = 1,5 |
в) |x – 2| < 0,5 |
д) |х – 3| > 3 |
б) |x + 1,5| = 2 |
г) |x + 2,5| < 2,5 |
е) |x + 2| > l,7. |
Задание 4. Расстояние между точками, изображающими действительные числа α и β на координатной прямой, равно | α – β |. Пользуясь этим, решите уравнение:
а) |x – l| = 3 |
д) |х — 1| + |x – 2| = 3 |
б) |x| + |x – 3| = 5 |
е) |x + 3| - |x – 1| = 4 |
в) |x – 6| + |x – 6| = 0 |
ж) |x – 1| = 2 |x – 4| |
г) |x – 2| + |3 – x| = 6 |
з) |x – 1| + |х – 2| = |x – 3|.
|
Задание 5. Докажите, что
а)
;
б)
в)
.
Задание 6.
Докажите, что
тогда и только тогда, когда
.
Задание 7. Докажите, что:
а)
;
б)
;
в) .