Практическая часть

Задание 1. Продумайте ответы на следующие вопросы:

1. Какие числа называются иррациональными? Приведите примеры иррациональных чисел.

2. Может ли рациональное число быть равно иррациональному?

3. Назовите:

а) два иррациональных числа меньше 5;

б) два отрицательных иррациональных числа;

в) два иррациональных числа, расположенных между числами -2 и – 1.

Задание 2. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже.

Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник».

1. Укажите среди данных чисел натуральные, рациональные, иррациональные: 0,5; –6,2; ; p; ; ; 2; 9; ; ; 0,22212(221); 2,01001(0001).

2. Представьте число в виде бесконечной десятичной дроби:

а) ; б) 0,(32); в) .

3. Сравните действительные числа:

а) 0,(21) и 0,21; б) и 1,375; в) p и 3,1416.

4. Назовите:

а) два иррациональных числа меньших 7;

б) два иррациональных числа, расположенных между числами – 3 и –1.

5. Может ли рациональное число быть равным иррациональному ?

6. Назовите десятичные приближения с недостатком и с избытком с точностью до 0,01 числа:

а) 14,372; б) 2,1264; в) 0,1751.

7. Какие из следующих чисел являются рациональными, какие – иррациональными:

а) ; в) 0; д) 0,444…;

б) ; г) –; е) 3,010010001… ?

8. Найдите множество чисел, состоящее из объединения (пересечения) множества рациональных и множества иррациональных чисел.

9. Сравните числа 0,1845 и 0,184184…; p и 3.1415.

10. В числе 0,12345678910111213…30 вычеркнуть после запятой сорок семь цифр так, чтобы полученное число было наибольшим.

11. Каким из множеств принадлежит число 0,(3); R; Z; N; Q; Q I R₊; Q I R; R₊; R?

12. Расположите в порядке возрастания следующие числа: 0,466; ; 0,4636363…; 0,463736; 0,4656565… .

.

13. Объясните, с какой закономерностью идут цифры в бесконечной десятичной дроби:

а) 5,3287177177177…;

б) 0,1010010001000010…;

в) 1,252255222555222255…;

г) 0,410414104141410414…;

д) 0,14916221364964… .

14. Не выполняя деления, скажите, конечной или бесконечной десятичной дробью можно выразить данную обыкновенную дробь: ; ; ; ; ; .

15. При каких значениях a и b верны равенства a + b = 0, a – b = 0, a · b = 0, = 0 ?

16. Представьте число в виде бесконечной десятичной дроби:

а) ; в) –; д) 3; ж) 0,(66);

б) ; г) ; е) 0,(5); з) 1,(37).

17. Сравните действительные числа:

а) 3,5732218904 и 3,5723218904;

б) 7,2537(4) и 7,253745;

в) – и – .

18. Укажите число х, находящееся в интервале:

а) х Î N, < х < ;

б) х Î R, 1,45 < х < 1,46;

в) х Î R, < х < .

19. Приведите пример двух иррациональных чисел таких, что:

а) их сумма (разность) – иррациональное число;

б) их сумма (разность) – рациональное число;

в) их произведение (частное) – иррациональное число;

г) их произведение (частное) – рациональное число.

20. Может ли:

а) сумма двух рациональных чисел быть числом иррациональным;

б) сумма двух иррациональных чисел быть числом рациональным ?

в) сумма двух действительных чисел быть рациональным числом?

21. При каких действительных значениях х имеет место равенство х + ïхï = 0 ?

Задание 3. Докажите иррациональность числа:

а) ; б) ; в) ; г) ; д) .

Задание 4. Докажите, что числа 2,6 и 2,7 являются десятичными приближениями соответственно с недостатком и с избытком числа с точностью до 0,1.

Задание 5. Найдите три первых десятичных знака бесконечной десятичной дроби, выражающей результат действия:

а) ; в) ; д) ; ж) ;

б) ; г) : е) : з) .

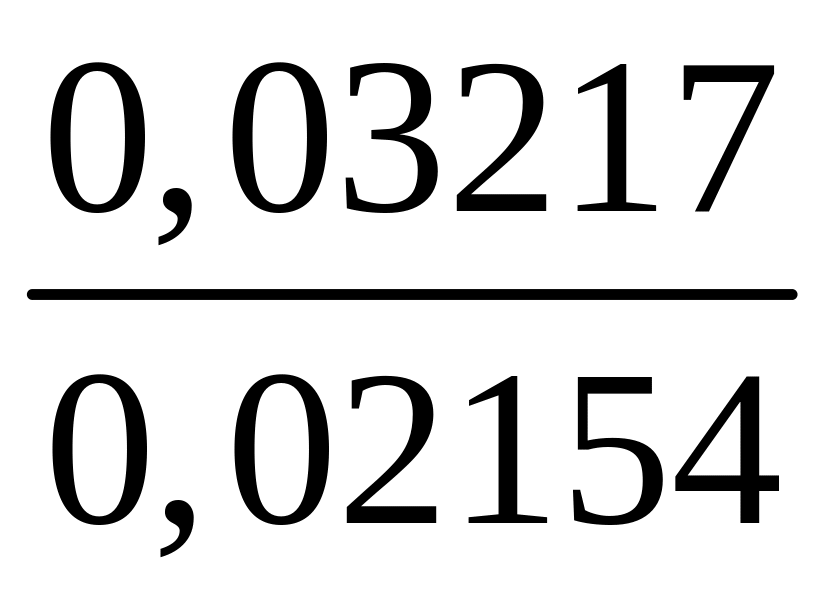Задание 6. Докажите, что сумма разность, произведение и частное двух действительных чисел, одно из которых рациональное число, отличное от нуля, а другое — иррациональное , являются иррациональными числами.

Задание 7. Может ли сумма рационального и иррационального чисел быть рациональным числом ?

Задание 8. Может ли сумма двух иррациональных чисел быть рациональным числом ?

Задание 9. Докажите, что сумма, разность, произведение и частное двух действительных чисел, одно из которых рациональное, а другое — иррациональное, является иррациональным числом.

Задение 10. Могут ли быть иррациональными числа а и b, если рациональны числа:

а) а + а и а – b; в) аb и ;

б) а – b и аb; г) а + b и

Задание 11. Докажите, что сумма, разность и произведение чисел вида , где a Q и b Q также могут быть представлены в таком же виде.

Задание 12. Число r— рациональное, число α – иррациональное. Рационально или иррационально число:

а) б) r +

Задание 13. а) Докажите, что – иррациональное чис­ло, если –иррациональное число (m N, n N).

б) Верно ли обратное утверждение ?

Задание 14. Числа а, b и – рациональны. Дока­жите, что и – рациональные числа.

Задание 15. Докажите иррациональность числа:

а) ; б) ; в) 1– ; г) 2 + .