Рубрика “Ваш помошник”

К заданию 2. Ответы к устным упражнениям.

1. а) ; б) ; в) –; г) –; д) , где n Î N.

2. а) 6; 17; б) –80; –2; 0; 6; 17; в) –80; –12,5; –2; –; 0; 20;

г) –12,5; –; 20.

3. а) неверно; верно; верно; б) неверно; неверно; верно;

в) верно; верно; верно.

4. Множеству рациональных чисел.

5. и –1, так как + (–1) = × (–1) = : (–1) = –.

6. Например: а) 6,01; 6,02; 6,03; б) –0,01; –0,001; –0,005;

в) –200,5; –200,4; – 200,3; г) 0,3; 0,32; 0,38.

7. а) k = 0, q – любое рациональное число, отличное от 0;

б) k = q, q ¹ 0; в) k = –q, q ¹ 0; г) k > q > 0 либо k < q < 0;

д) 0 < k < q либо q < k < 0; е) таких рациональных чисел k и q не существует.

8. Нет.

9. 1 – = 0,9.

10. а) –5; 5; б) –2; 2; в) –; .

11. Докательство: а) 11 > 0 и 11² = 121, следовательно, = 11; б) 20 > 0 и 20² = 400, следовательно, = 20.

12. а) Да; нет; да; б) да; нет; да; да.

13. а) 5; б) 7; в) 100; г) 0,9; д) 0,4; е) 0,2; ж) ; з) 1; и) 1.

16. а) 9 > 0 и 9² = 81.

17. а) 5; б) 11; в) 0,6; г) 1,6; д) ; е) .

18. а) 10; б) 40; в) ; г) ; д) 0,9; е) ; ж) 0,1; з) 0,001.

19. а) 70 = 2 × 5 × 7, не обращается;

б) 26 = 2 × 13, не обращается;

в) 16 = 2 × 2 × 2 × 2, обращается;

г) 50 = 2 × 5², обращается.

20. = 0,5000…; = 0,25000…; = 0,125000…; = 0,2333… .

21. 5,74444…

22. = 0,(2); = 0,(6); = 0,1(6).

23. 0,(4) = ; 0,(5) = ; 0,(21) = ; 1,(137) = .

К заданию 6. а) 8,64; б) 13; в) ; г) 9.

К заданию 7. 9.

К заданию 8. а) ; б) .

К заданию 10. а) 25; б) 0,01; в) 0,12; г) 21 д) 0,001024

К заданию 11. а) 12; б) 9.

К заданию 12. 200.

УЭ-2. Действительные числа

Ваша цель: углубление и расширение знаний о множестве действительных чисел.

Входная информация

Понятие действительного числа. Число, которое может быть представлено в виде бесконечной десятичной непериодической дроби, называется иррациональным.

Примерами иррациональных чисел являются:

1. число 7,030033000333…

2. число , бесконечная непериодическая дробь

3,141592653689793…;

3) число 0,101001000100001…, у которого за каждой единицей идет группа нулей, содержащая на один больше, чем предыдущая группа.

Множество бесконечных непериодических дробей (положительных и отрицательных) образует множество иррациональных чисел.

Объединение множеств рациональных и иррациональных чисел образует множество действительных чисел. Это множество обозначают буквой R.

Любое действительное число представляется в виде бесконечной десятичной дроби: , … …, где – целое число, , , , …, – цифры.

Соотношения между числовыми множествами N, Z, Q и R. Оно представлено на схеме :

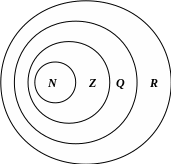
Разбиение множества всех действительных чисел на непересекающиеся подмножества показано на схеме 2.

Целые отрица-тельные числа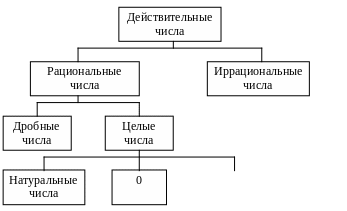

Понятие противоположных чисел. Два действительных числа называют противоположными, если их сумма равна 0.

Например, – 3 и 3; и – противоположные числа.

Число 0 противоположно самому себе.

Понятие взаимно обратных действительных чисел. Взаимно обратными числами называют два действительных числа, произведение которых равно 1.

Например, и ; и ; и – взаимно обратные числа.

Число 1 обратно самому себе. Для числа 0 обратного числа не существует.

Сравнение двух действительных чисел. Число больше числа , и пишут > , если разность – положительное число; если же разность – отрицательное число, то говорят, что число меньше числа , и пишут < ; число равно числу , если .

Для любых заданных действительных чисел и имеет место одно и только одно из соотношений: < , , > .

При сравнении двух бесконечных десятичных дробей (не имеющих периода 9) пользуются следующим правилом.

, … < , …,

если и < при всех < ( = 0, 1, 2, 3, …).

Заметим, что если целые части двух десятичных дробей разные, то та дробь больше, у которой целая часть больше. Если целые части одинаковы, то надо обратиться к наименьшему разряду, для которого цифры дробей различны: та из дробей больше, у которой цифра этого разряда больше.

Действия над действительными числами. Действительные числа можно складывать, вычитать, умножать и делить.

При выполнении действий в практических задачах действительные числа заменяют их приближенными значениями. Повышая точность, с которой берутся приближенные значения, получают более точное значение результата.

Свойства действий над действительными числами:

1. – переместительный закон сложения;

2. – сочетательный закон сложения;

3. ;

4. ;

5. – переместительный закон умножения;

6. – сочетательный закон умножения;

7. – распределительный закон умножения относительно сложения;

8. ;

9. 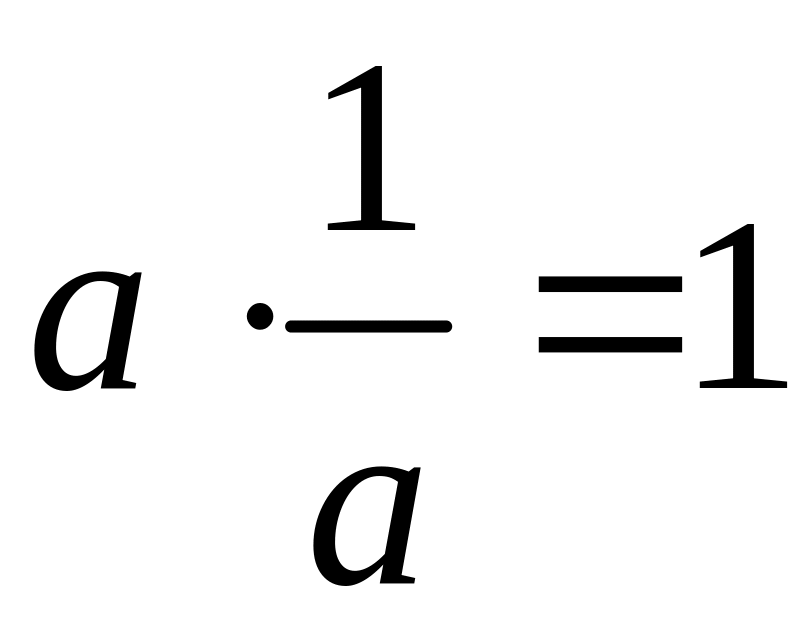, где ;

10. .

Понятия среднего арифметического и среднего геометрического действительных чисел. Средним арифметическим нескольких чисел называют число, которое получается при делении суммы этих чисел на число слагаемых.

Например, среднее арифметическое чисел 30, 70 и 95 есть число, равное числу 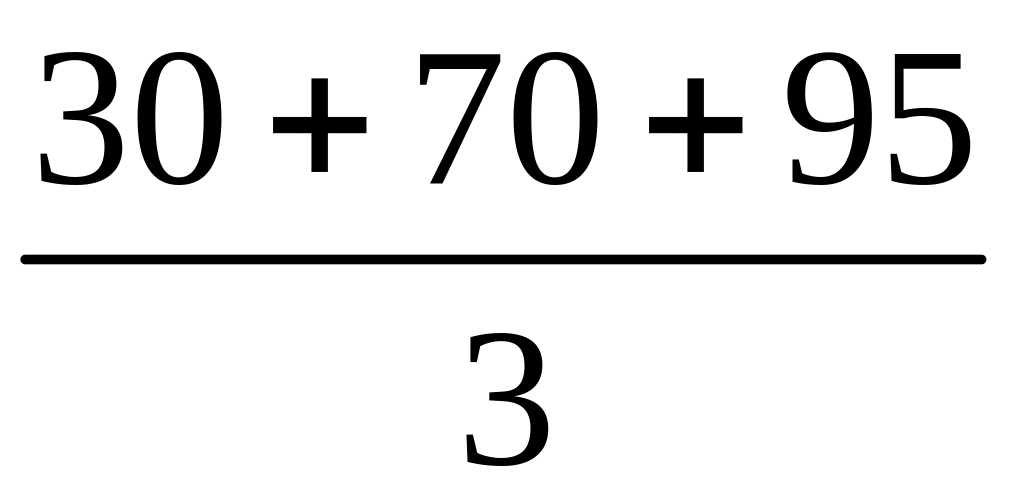, т.е. числу 65.

Средним геометрическим положительных чисел , , …, называют корень -ой степени из произведения этих чисел, т.е. .

Обобщенное неравенство Коши имеет вид:

.
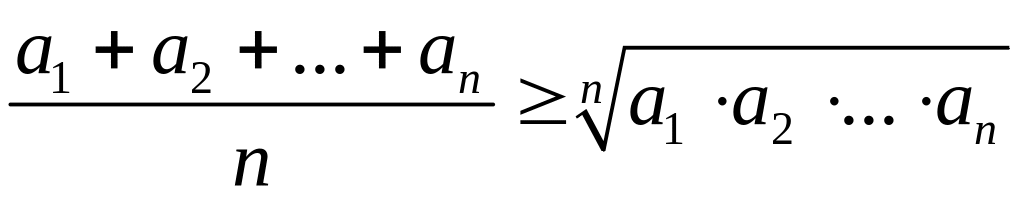