Практическая часть
Задание 1. Продумайте ответы на следующие вопросы:
Какие числа составляют множество всех рациональных чисел? Как обозначается это множество? Приведите примеры рациональных чисел.
Существует ли взаимно однозначное соответствие между множеством всех рациональных чисел и множеством всех точек на координатной прямой?
Всегда ли выполнимы действия сложения, умножения, вычитания и деления на множестве Q?
Что называется арифметическим квадратным корнем? Сколько существует арифметических квадратных корней из неотрицательного рационального числа а?
Всегда ли имеет уравнение
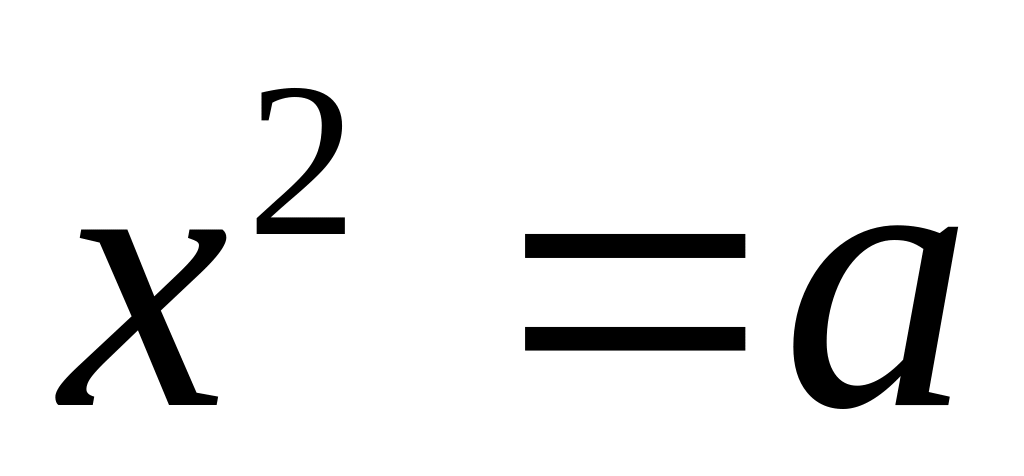рациональные корни при a
> 0, a = 0, a
< 0 и, если имеет, то сколько?Могут ли быть равными: а) квадраты неравных чисел; б) арифметические квадратные корни из неравных чисел?
Назовите два рациональных числа, расположенных между числами – 0,13427 и 0.
Задание 2. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже.
Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник».
Устные упражнения
1. Представьте в виде отношения целого числа к натуральному следующие числа: а) 1; б) 0,4; в) –1; г) –17; д) 0.
2. Какие из чисел –80; –12,5; –2; –; 0; 6; 17; 20 являются: а) натуральными; б) целыми; в) рациональными, но не натуральными; г) рациональными, но не целыми ?
3. Верно ли, что:
а) –4 Î N; –4 Î Z; –4 Î Q;
б) 3,6 Î N; 3,6 Î Z; 3,6 Î Q;
в) 14 Î N; 14 Î Z; 14 Î Q.
4. Пусть х Î Q, у Î Q. Какому из числовых множеств принадлежит х + у; х – у; ху; ?
5. Укажите два таких рациональных числа, чтобы их сумма, произведение, частное были равны между собой.
6. Укажите несколько рациональных чисел, заключенных между:
а) 6 и 6,1; б) –0,02 и 0; в) –201 и –200; г) и .
7. Укажите такие рациональные числа k и q, при которых имеет место соотношение:
а) = 0; в) = –1; д) < 1;
б) = 1; г) > 1; е) · > 1.
8. Могут ли два взаимно обратных числа иметь противоположные знаки ?
9. Вычислите:
+ + + … + + .
10. Решите уравнение:
а) х2 = 25; б) х2 = 2; в) х2 = 3.
11. Докажите, что верно равенство:
а) = 11; б) = 20; в) = 0,5; г) = 0,3.
12. Какие из данных выражений имеют смысл:
а) , , –;
б) , , –, –.
13. Найдите значение корня:
а) ; г) ; ж) ;
б) ; д) ; з) ;
в) ; е) ; и) .
14. Почему уравнение не имеет корней:
а) = –3; в) – = 3;
б) + 2 = 0; г) 3 = –12 ?
15. Докажите, что
а) число 7 есть арифметический квадратный корень из 49;
б) число 0,5 есть арифметический квадратный корень из 0,25;
в) число –1,3 не является арифметическим квадратным корнем из 1,69.
16. Докажите, что:
а) = 9; в) = 4,1;
б) = 2,2; г) = 0,18.
17. Вычислите арифметический квадратный корень из числа:
а) 25; б) 121; в) 0,36; г) 2,56; д) ; е) 6.
18. Найдите значение корня:
а) ; в) ; д) ; ж) ;
б) ; г) ; е) ; з) .
19. Даны дроби а) ; б) ; в) ; г) . Не пользуясь алгоритмом деления, выясните, какие из обыкновенных дробей обращаются в конечные десятичные дроби.
20. Представьте в виде бесконечной десятичной дроби рациональное число: ; ; ; .
21. Каково наименьшее рациональное число, большее числа 5,7 в бесконечную запись которого не входят цифры 0, 1, 2, 3 ?
22. Записать рациональное число в виде периодический дроби: ; ; .
23. Представьте в виде обыкновенной дроби: 0,(4); 0,(5); 0,(21); 1,(137).
Задание
3. Докажите, что если a
и b – рациональные числа
и
,
то число
лежит между ними.
Задание 4. Докажите, что между любыми двумя рациональными числами содержится бесконечное множество рациональных чисел.
Задание 5.Укажите несколько рациональных чисел, заключенных между:
а) 6 и 6,1; б) –0,01 и
0; в) –102 и –101; г)
и
.
Задание 6. Найдите х из пропорции:
а)
; в)
;
б)
; г)
.
Задание 7.
Найдите х из пропорции:
.
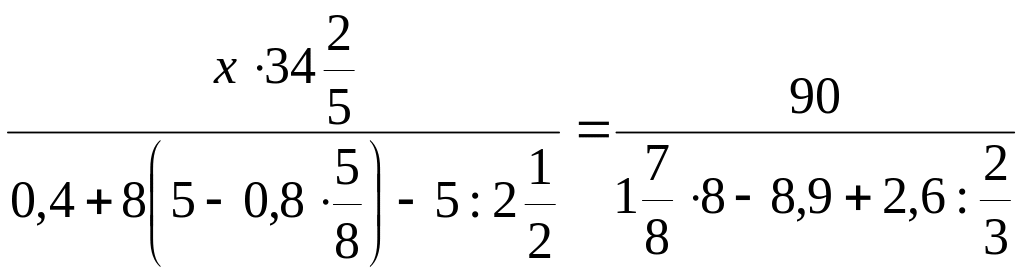Задание 8. Вычислите:
а)
;
б)
.
Задание 9. Вычислите:
а)
;
б)
;
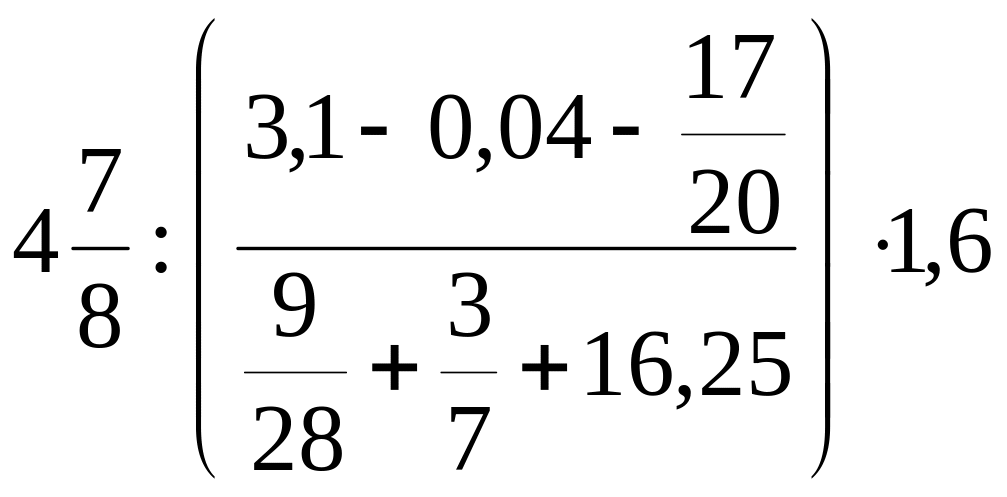в)
.
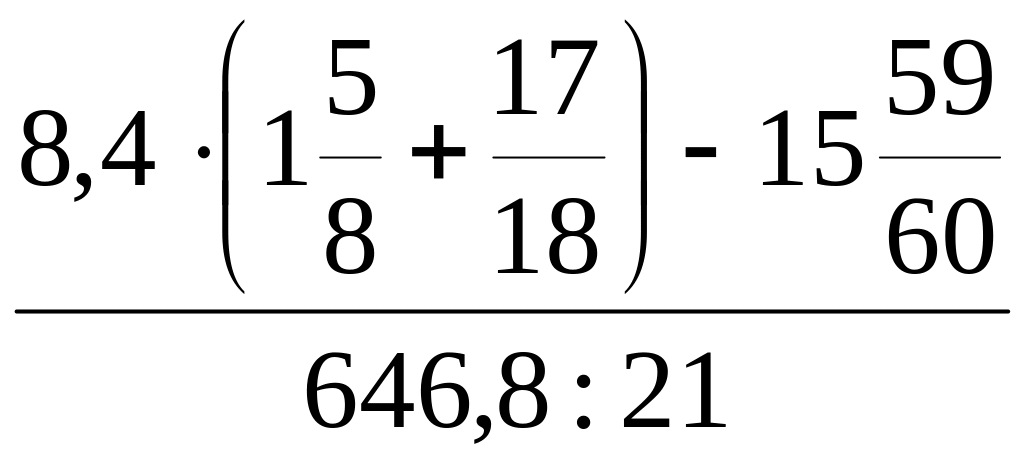Задание 10. Вычислите:
а)
;
б)
;
в)
;
г)
;
д)
.
Задание 11. Вычислите:
а)
;
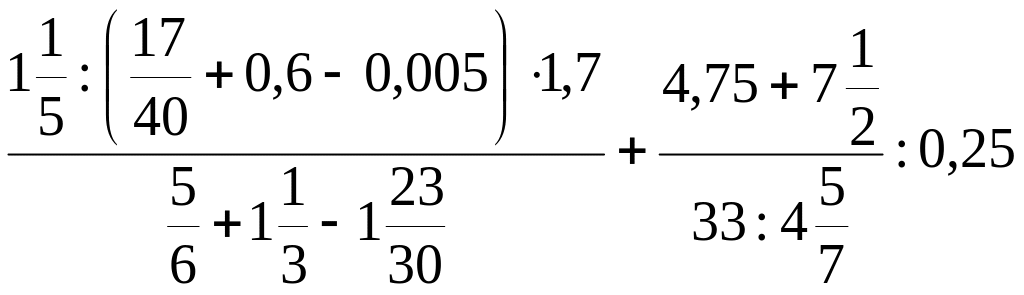б)
.
Задание
12.Найдите число, 7,5 % которого равно
А, где
.
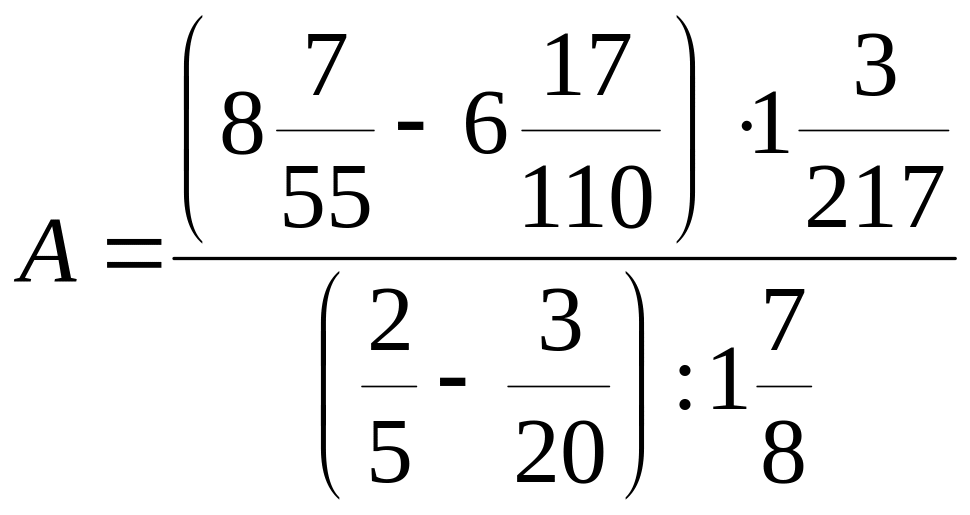