Краткие исторические сведения о неравенствах

Понятие неравенства, как и понятие равенства, возникло в глубокой древности. Без понятий «больше» и «меньше» нельзя было осмыслить понятия равенства, тождества, уравнения. Ряд неравенств приводит в своем знаменитом трактате «Начала» Евклид. Он, например, доказывает, что верно неравенство , где , т. е. среднее геометрическое двух неотрицательных чисел не больше их среднего арифметического. В «Математическом собрании» Паппа Александрийского (III в.) доказывается, что если ( — положительные числа), то .

При этом все рассуждения проводились словесно с опорой в большинстве случаев на геометрическую терминологию. Современные знаки неравенства появились лишь в XVII — XVIII вв. Знаки < и > ввел английский математик Т. Гарриот (1560—1621). Символы и были введены в 1734 г. французским физиком и математиком Пьером Буге (1698—1758). Позже их стали записывать так: , .

Неравенства и системы неравенств широко используются как в теоретических исследованиях, так и при решении практических задач.

Интересно знать

Известный русский писатель А. С. Грибоедов, поступив в Московский университет, окончил за шесть с половиной лет курс трех факультетов: словесного, юридического и физико-математического.

Профессор математики Оксфордского университета Чарльз Лютвидж Латвидж Доджсон (1832—1898) издал под именем Льюиса Кэрролла ряд детских книг. На русском языке неоднократно издавались «Алиса в Стране Чудес» и «Алиса в Зазеркалье».

Кто сильнее?

Однажды в минуты отдыха друзья-мушкетеры Атос, Портос, Арамис и д'Артаньян решили немного поразвлечься в перетягивании каната. Портос с д'Артаньяном легко перетянули Атоса с Арамисом. Но когда Портос стал в паре с Атосом, то победа над Арамисом с д'Артаньяном досталась им уже не так легко. А когда Портос с Арамисом выступили против Атоса с д'Артаньяном, то никакая из этих пар не смогла одолеть другую.

Определите, как мушкетеры распределяются по силе.

Нематематики о математике

Процветание и совершенство математики тесно связано с благосостоянием государства.

Наполеон

Математики похожи на французов: что бы вы ни сказали, они все переведут на свой собственный язык. Получится нечто противоположное.

Гёте

Модуль 2.

Действительные числа

УЭ-1. Рациональные числа

Ваша цель: систематизировать и обобщить знания по теме «Рациональные числа»

Входная информация

Понятие рационального числа. Рациональным числом называют число, которое можно представить в виде , где , .

Числа, которые можно записать в виде дроби, называют рациональными числами. Всякое целое число является рациональным. Например, , , .

Название «рациональное число» происходит от латинского слова ratio – отношение (рациональное число – отношение целых чисел).

Множество рациональных чисел состоит из всех целых чисел, всех дробных чисел, положительных и отрицательных, и числа нуль. Множество рациональных чисел обозначают Q. Отметим, что .

Арифметический квадратный корень из рационального числа. Напомним определения понятия арифметического квадратного корня.

Арифметическим квадратным корнем из рационального числа а называется неотрицательное число, квадрат которого равен а.

Арифметический квадратный корень из числа а обозначают так: . Знак называется знаком арифметического квадратного корня, число, стоящее под знаком корня, называется подкоренным числом. Запись читается: «Арифметический квадратный корень из числа а», либо «Арифметическое значение квадратного корня из числа а».

Выполняя действие извлечения квадратного корня из рационального числа, не всегда получают рациональное число, т. е. операция извлечения квадратного корня не всегда выполняется на множестве Q. Нельзя извлечь квадратный корень из отрицательного рационального числа, ибо квадрат любого рационального числа не может быть отрицательным. Оказывается, что и не из каждого рационального положительного числа можно извлечь рациональный квадратный корень. Этот факт подтверждает теоремой:

Не существует рационального числа, квадрат которого равен. 2.

Можно доказать, что не существует рационального числа, квадрат которого равен 3, 5, 7, 10

Представление рационального числа в виде бесконечной десятичной периодической дроби. Напомним основные правила.

Правила обращения периодической десятичной дроби в обыкновенную дробь. Не существует правил действий над периодическими дробями. Поэтому их обращают в обыкновенные дроби по следующим правилам.

Правило 1. Правильная чистая периодическая дробь равна обыкновенной, числителем которой является период периодической дроби, а знаменатель состоит из стольких девяток, сколько цифр в периоде.

Например: ; .

Правило 2. Правильная смешанная периодическая дробь равна обыкновенной, в числителе которой находится разность числа, стоящего до второго периода, и числа, стоящего до первого периода, а в знаменателе столько девяток, сколько цифр в периоде, и столько нулей, сколько цифр между запятой и первым периодом.

Например: ;

.

Пример 1. Вычислить:

.

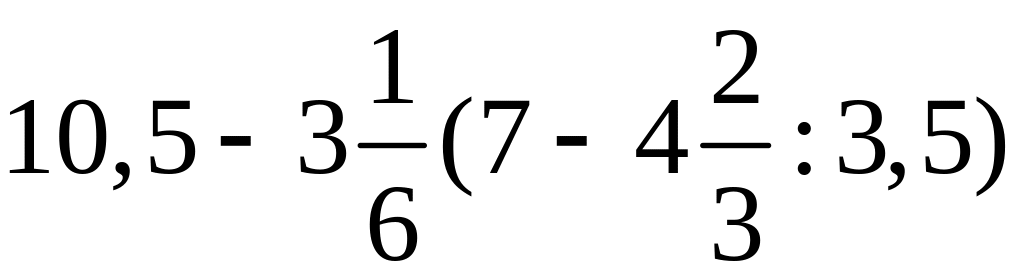Решение.

1) ;

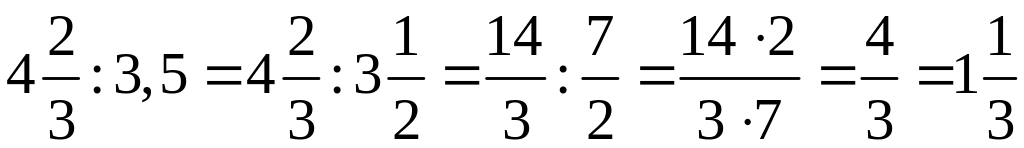2) ;

3) ;

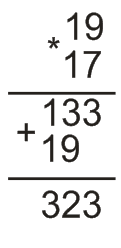
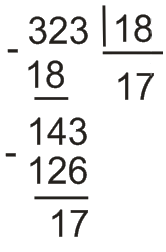
4)

.

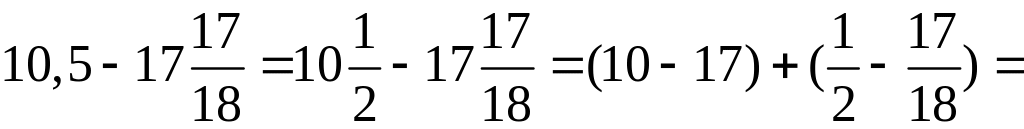
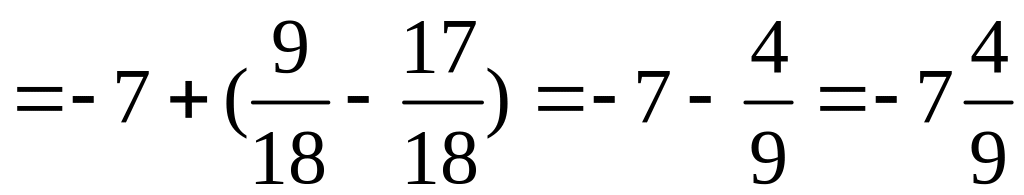Ответ: .