Определение 2. Функция диф-ма в некотрой области, если она диф-ема в каждой точке этой области.

Определение 3. Если функция диф-ма, то каждое изслагаемых A_i∆x_i называется главным диф-лом х_i. A_i∆x_i=dx_if.

Билет Ш(3).

§5. Производные по направлению. Частные производные функций нескольких действительных переменных, теорема о дифференцируемости.

Определение 1. F:y=f(р) если  ,(PP₀,PS), то этот предел называется производной функции по заданному направлению и обозначается символом f(P₀)/S.

Теорема о диф-ти.

Если функция диф-ма в некоторой точке, то у нее  производная по  направлению.

Док-во. Пусть функция диф-ма, тогда по определению полное приращение ∆f(P₀)=(i=1)(n)A_i(x_i-x_i0)+(∆). =(i=1)(n)∆x_i/∆+(∆), так как ∆=Р₀Р. если Р₀Р={∆x₁, ∆x₂, …, ∆x_n} – то P₀P/P₀P=S – единичный вектор, направляющий вектор прямой, проходящей через Р и Р₀.

Определение 2. Пусть функция определена в пространстве Rⁿ и пусть в пространстве введена артонормированная декартова система координат. Пусть е_к-еденичный вектор(репер).

Частная производная по переменной х_к есть производная по направлению, гда направление определяет S=e_k.

Билет Ш(4).

§9. Градиент.

Определение 1. Пусть z=z(x,y), тогда вектор с компонентами =grad(z)(градиент функ.).

Теорема 1. Gradf указывает направление максимальной скорости роста функции, численно равен по модулю значению максимальной скорости роста и является ортогональным поверхности уровня, проходящего через точку, где grad вычисляется.

Док-во. f/S=(gradf,S)=gradfS*cosץ=gradץ*cosץgradf_P0=числовсе зависит от ץ  если cosץ=1 то есть или max или min значение скорости роста.

Следствие 2. Grad является аналогом первой производной.

Билет Ш(5).

§6. Сложные функции. Производные сложных функций.

Определение 1. Говорят что задана некоторая F(P), точка PR²:z=f(U,V), где U=ץ(x,y), V=(x,y).

U,V-промежуточные или вспомогательные переменные.

Теорема 1. Пусть задана F(x,y) : z=f(U,V), U=ץ(x,y), V=(x,y), тогда если  и ץ непрерывно диф-мы в окрестности некоторой точки (х₀,у₀), а функция f как функция дыух промежуточных переменных непрерывно дифференцируема в окрестности точки (U₀,V₀) определяемыми соотношениями U₀=ץ((x₀,y₀), V₀=(x₀,y₀), то  частные производные сложной функции по незавсисимым переменным х и у равные соответственно……………………………………..

Док-во. Пусть х₀, х₀+∆х-два значения переменной х в U(x₀,y₀), пусть при этом у₀ фиксированаץ,  имеют частное приращение в окрестности указанной точки, равные соответственно ∆_xU=ץ(x₀+∆xy₀)-f(x₀,y₀)=U(x₀+∆x,y₀)-U(x₀,y₀), соответственно ∆_xV=V(x₀+∆x,y₀)-V(x₀,y₀).

Тогда в окрестности точки (U₀,V₀) следующая функция имеет полное приращение ∆z=f(U₀+∆_xU,V₀+∆_xV)-f(U₀,V₀). )., где ∆= . (∆x0), но так как (∆x0; ∆_XU,∆_XV0).

Определение 2. Пусть F: z=f(U,V), U=U(x), V=V(x), тогда .

Определение. Говорят, что функция задана неявно, если она задана при помощи уравнения содержащего (п+1) переменную.

Билет Ш(6).

§7. Функции, заданные неявно.

Теорема 1.пусть f задна неявно при помощи уравнения F(x,y), тогда если функция является диф-мой, как функция 2-х действительных переменных в окрестности некоторой точки с координатами (х₀,у₀). У функции  производная .

Теорема 2. Пусть F(x,y,z)=0, z=z(x,y) тогда если F диф-ма по переменным x,y и z в окрестности некоторой точки (x₀,y₀z₀(x₀y₀)), то у функции  в частности .

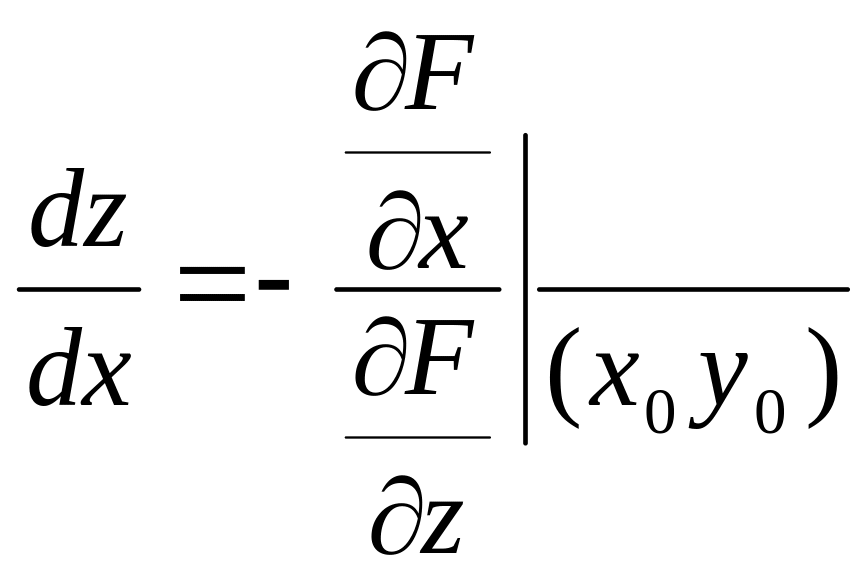Док-во. Пусть в окрестности рассматриваемой точки выбраны два значения переменной x₀ и y₀ и x₀+∆x; у₀ фиксирована тогда z=z(x,y) – функция одной действительной переменной .

Билет Ш(7).