§8. Односторонние пределы функции.

Теорема. Для того, чтобы в окрестности точки х=а у функции  предел, необходимо и лостаточно, чтобы в окрестности этой точки -ли оба односторонних предела, равные между собой.

§9. Определение 1. Называется 1-ым замечательным пределом.

Определение 2. Так как х в окружности точки 0 бесконечно малая, то .

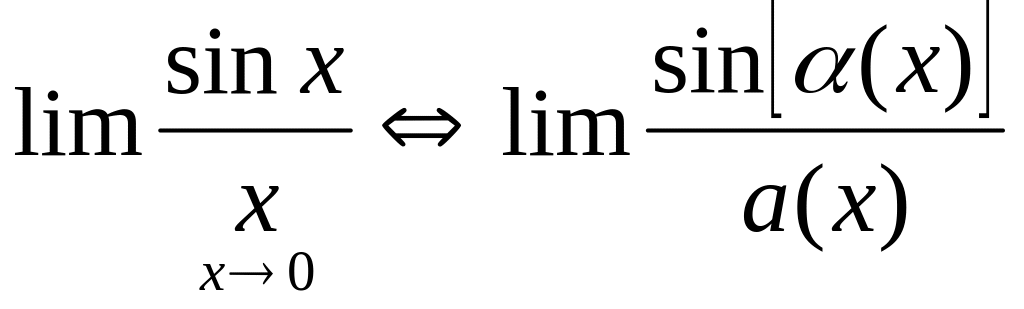Определение 3. Lim(1+ )ⁿ (n)=e=2,718281828459045… - 2-ой замечательный предел.

Теорема 1.пусть имеется степенно-показательная функция F:y=f(x), при этом limf(x)^g(x)=1 (x0).

limg(x)=, то [1^]=lim(1+(x))=e ((x)0) – 2-ой замечательный предел.

Билет I(6).

§10. Непрерывность функции.

Свойтва функций, непрерывных на некоторых множествах.

Определение 1. F: y=f(x), D(f)=. Х₀ – некоторое значение переменной х, х₀D(f), тогда приращением аргумента или независимой переменной называется разность х-х₀=∆х, хD(f) и приращением функции относительно рассматриваемого приращения аргумента называется разность f(x)-f(x₀)=∆f(x₀).

Определение 2. Функция F: y=f(x), D(f)= называется непрерывной в точке х=х₀ если предел приращения этой функции lim∆f(x₀)=0 (∆x0). (∆х – б.м)

Определение 3. Пусть  есть некоторое множество, тогда если функция непрерывна в каждой точке этого множества, то функция называется непрерывно на множестве и при этом fC_x.

1))) свойства непрерывных функций.

Теорема 1. Есил функции f, g, …, непрерывны на одном и том же множестве, то:

любая их линейная комбинация будет функцией непрерывной на этом множестве.

Любая функция f(x)/g(x) будет функцией непрерывной на множестве \{g(x)=0} (функция в знаменателе =0).

Теорема 2. Если функция непрерывна в точке, то limf(x)=f(limx) (xx₀).

Теорема 3. Если f(x) непрерывна на некотором множестве, то график функции представляет непрерывное множество точек на числовой плоскости и следовательно, если введена та или иная система координат, то каждому графику в этой системе координат может быть поставлена во взаимно однозначное соответствие некоторая линия, являющаяся графиком изображающим рассматриваемые функции Gr(f)={(x, y)R²}.

§11. Классификация точек разрыва в функциях.

Определение 1. Если в какой-либо из точек нарушено хотя бы одно условие непрерывности функции, то указанное значение переменной х называется точкой разрыва функции, но при этом:

если не  f(x₀), но  оба односторонних предела, равные между собой, точка х₀ называется тогда точкой устранимого разрыва функции.

если же  оба односторонниз предела, но не раваные между собой, то точка х₀ называется точкой разрыва первого рода.

если же хотя бы один из односторонних пределов есть б.б. или же не  вовсе, то точка разрыва называется точкой разрыва второго рода.

Билет II(1).

§1. Дифференцируемость функции. Понятие дифференциала. Теорема о непрерывности.

Определение 1. F:y=f(x), называется дифференцируемой в точке х₀, если приращение функции ∆f(x₀) может быть представлено в виде суммы 2-х слагаемых, 1-ое из которых является линейной относительно переменной ∆х функцией, а 2-ое есть б.м. более высокого порядка малости: ∆f(x₀)=A∆x+(∆x). Если приращение функции может быть представлено в таком виде, то функция называется дифференцируемой.

Определение 2. Если функция дифференцируема в каждой точке множества, функция называется дифференцируемой на множестве fC_x⁽¹⁾.

Определение 3. Первое слагаемое в разложении приращения функции, если она дифференцируема, называется главной линейной частью разложения или дифференциалом функции 1-ой действительной переменной.

Теорема. В каждой точке, в которой функция дифференцируема, она и непрерывна.

Док-во. Пусть функция дифференцируема в точке 0, тогда её приращение может быть записано по определению: ∆f(x₀)=A∆x+(∆x), ∆х=[0]/хх₀.  lim∆f=0 (∆x0) следовательно f(x) непрерывна. Y=x, x=0, ∆y(0)={0+∆x=0=∆x0 (∆x0). ∆y=(1*∆x;x>0;;; -1*∆x;x<0).

Билет II(2).