§2 Производная. Односторонняя производная. Теорема о дифференцируемости.

Определение 1. Если ∆f есть приращение функции относительно приращения независимой переменной ∆х и если  (∆x0), то указанный предел называется производной функции в точке х₀.

Определение 2. Если  правосторонний предел lim (∆х0, x>x₀), то этот предел называется правосторонней производной в точке х₀. lim (∆х0, x<x₀). Для того, чтобы  производная функция, необходимо и достаточно, чтобы у функции  в рассматриваемой точке обе односторонние производных, равные между собой.

Теорема о дифференцируемости.

Для того, чтобы функция была дифференцируема в точке или на области, необходимо и достаточно, чтобы у функции  производная.

Док-во. Необходимость: пусть f:y>f(x) дифференцируемав точке х₀, тогда по определению  такая окрестность указанной точки, что для  значений х из указанной окрестности приращение функции может быть представлено в виде суммы 2-х слагаемых. хU(x₀), ∆f=A∆x+(∆x), ∆x=x-x₀, но тогда  lim (∆х0). Пусть у функции  производная в рассматриваемой точке, тогда по определению производной  lim (∆х0). То тогда по основной теореме о пределах  такая окресность, в которой =f^’(x₀)+(∆x), (∆x):=[0]. Тогда приращение функции может быть записано как: ∆f=f^’(x₀)∆x+(∆x)∆x. 1-ое слагаемое – линейная относительно ∆x часть приращения а предел lim (∆x0).

Следовательно тогда, по классификации б.м-ых, 2-ое слагаемое записанное в приращении, есть (∆x) следовательно функция дифференцируема.

Билет II(3).

Свойства: 1) dC=0; 2) d(f+g)=df+dg; 3) d(f(x)*g(x))=df*g(x)+f(x)*dg; 4) d .

Билет II(4).

§3. Сложные функции. Производные сложных функций.

Определение 1. Задана сложная функция F(x) от независимой переменной х, если она задана при помощи следующих последовательных правил: y=f(U), U=(x), DF={xR:xD(),UD(f)}.

Теорема о производной сложной функции.

Пусть сложная функция задана F:y=f(U), U=(x), D(f) и пусть в окрестности точки х₀  непрерывная производная от функции , а в соответствии точки U₀=(x₀)  непрерывная производноая сложной функции по переменной х, которая может быть записана по правилу: . Док-во. В силу дифференцируемости функции в точке U₀,  такая U(U₀) что  UU_(U0) ∆f=f’_U(U₀)∆U+(∆U)x₀ .

В силу непрерывности функции , ∆х0, тогда и ∆U0, но тогда  (∆x0). (∆x0). ∆f∆y. Следовательно  .

§4. Логарифмические производные.

Определение 1. F(x):y=f(x)^g(x) называется степеннопоказательной.

Определение 2. F:y=f(x). Производная от натурального логарифма от записанного выражения называется логарифмичской производной, она не имеет обозначений.

Теорема. Если логарифмическая производная известна, то производная самой функции восстановляется однозначно.

Док-во. Lnf(x)_X’lny=lnf(x) по правилу дифференцирования сложной функции  1/y y’=(lnf(x)’_X, y_X’=y(lnf(x))’_X.

Билет II(5).

§5. Производная обратной функции.

Определение 1. Пусть на множестве  определена функция 1-ой дествительной переменной f:y=f(x). Пусть (f)=. Говорят, что на множестве  определена функция, обратная данной, если на множетстве  указан закон, правило по которому каждому значению переменной у ставится в соответствие единственное значение переменной х:y=f(x). При этом функция обратная к заданной обозначается символом f^-1.

Теорема 1. F и f^-1 –две взаимнообратные функции, тогда f(f^-1(y))=y, f^-1(f(x))=x.

Док-во. Очевидно! Так как f(f^-1(y))=f(x)=y, f^-1(y)=x..

§5. Теорема 2. Усли f:y=f(x) является монотонно возрастающей или монотонно убывающей на некотором множестве ,тогда на этом множестве у ыункции  обратная данной f^-1.

Теорема 3. Пусть у F  f^-1 тогда, если функция дифференцируема в окрестности точки х₀, обратная функция дифференцируема в окрестности точки. Y₀=f(x₀)  f_X’(x₀)*f_y^-1’(y₀)=1.

Док-во. В силу теоремы один имеет место равенство f(f^-1(y))=y или f^-1(f(x))=x. Рассмотрим отношение 2. F^-1(y), y=f(x); слева стоит сложная функция  по правилу дифференцированиясложных функций: f^-1_y(y₀)*y_x’=f_y^-1*f_x(x₀)=1.

§6. Определение 1. Функция задана параметрически, если она задана при помощи системы уравнений вида {x=(t), y=(t), tTCR и  хотя бы одна либо обратная к  либо к , при этом новая переменная t называется параметром.

Теорема 1. Функция задана параметрически, тогда если функции  и  дифференцируемы, то  производная по переменной х либо у заданная параметрически. При этом .

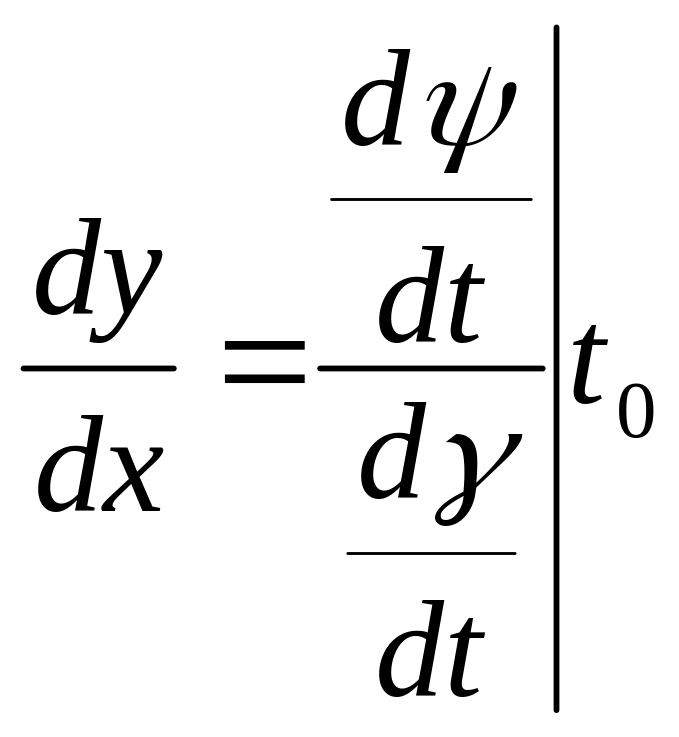Билет II(6).