13. Отклонение относительной частоты от постоянной вероятности. Закон больших чисел в формуле Бернулли.
Пусть
производится
независимых
испытаний, в каждом из которых вероятность
появления события
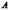равна
.
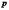Можно ли предвидеть, какова примерно
будет относительная частота появления
события?
Положительный ответ на этот вопрос дает теорема, доказанная Якобом Бернулли (опубликована в 1713г.), которая получила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Бернулли было сложным; простое доказательство дано П.Л. Чебышевым в 1846г.
Теорема Бернулли. Если в каждом из n независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.
Другими
словами, если
-
сколь угодно малое положительное число,
то при соблюдении условий теоремы имеет
место равенство
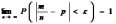
Задача 1. Длина изготовляемых изделий представляет случайную величину, среднее значение которой (математическое ожидание) равно 90 см. Дисперсия этой величины равна 0,0225. Оценить вероятность того, что длина изделия выразится числом, заключенным между 89,7 см. и 90,3 см.
Решение:
Случайная величина
-
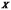длина изготовляемых изделий,
,
.
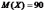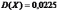По условию задачи случайная величина
заключена
между числами 89,7 и 90,3, т.е.
.
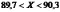Вычитая 90 из неравенства, получим:
или
.
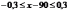Заменим
это неравенство равносильным
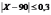и
применим к нему неравенство Чебышева,
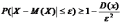
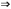
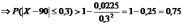т.е.:
,
т.е.
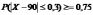
Задача 3. Вероятность вызревания кукурузного стебля с тремя початками равна ¾. Оценить вероятность того, что среди 3000 стеблей, доля стеблей с тремя початками будет по абсолютной величине отличаться от вероятности вызревания такого стебля не более, чем на 0,02.
Решение:
-
доля стеблей с тремя початками, т.е.
относительная частота.
;
;
,
.
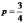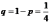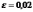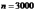Воспользуемся неравенством из теоремы Бернулли:
,
.
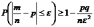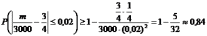Вероятность отклонения не менее 0,84, т.е. найдена нижняя граница вероятности.
14. Случайные величины: дискретные и непрерывные
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретные и непрерывные случайные величины
Вернемся к примерам, приведенным выше. В первом из них случайная величина Х могла принять одно из следующих возможных значений: О, 1, 2, ..., 100. Эти значения отделены одно от другого промежутками, в которых нет возможных значений X. Таким образом, в этом примере случайная величина принимает отдельные, изолированные возможные значения. Во втором и третьем примерах случайные величины могли принять любые из значений промежутков (а,b) и (c, d) . Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины.
Уже из сказанного можно заключить о целесообразности различать случайные величины, принимающие лишь отдельные, изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток.
Дискретной
(прерывной) называют случайную
величину, которая принимает отдельные,
изолированные возможные значения с
определенными вероятностями. Число
возможных значений дискретной случайной
величины может быть конечным или
бесконечным. Дадим более точное
определение :
Дискретной случайной величиной (ДСВ) называют такую величину, множество значений которой либо конечное, либо бесконечное, но счетное.
Непрерывной случайной величиной (НСВ) называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Множество возможных значений непрерывной случайной величины бесконечно и несчетно.