Пример 2-2. Расчёт неразветвлённой магнитной цепи.

Во всех участках неразветвлённой магнитной цепи, если пренебречь потоком рассеяния , проходит один и тот же поток (аналогия с током в неразветвлённой электрической цепи). Значение индуктивности и напряжённости магнитного поля могут быть различны. Однако цепь можно разбить на участки одинакового сечения и материала, в пределах каждого из которых напряжённость не меняется.

П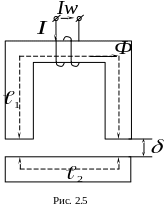 рямая задача

Рассмотрим в качестве примера электромагнит, притягивающий стальную пластину – якорь (рис. 2.5).

Дано: сердечник электромагнита из листовой стали, кривая намагничивания задана графически; якорь из литой стали, задана графически. Известны размеры магнитной цепи: . Задано число витков w и магнитный поток . Определить ток .

Решение

1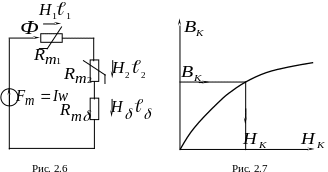 ) Разбить цепь на однородные участки, т. е. участки равного сечения и одинакового материала. В нашем примере таких участка три: сердечник, якорь и воздушный зазор. Их длины (они определяются по средней силовой линии) равны соответственно . Составить эквивалентную схему зам ещения (рис 2.6).

2) Для каждого участка определить магнитную индукцию:

где – поперечное сечение каждого участка.

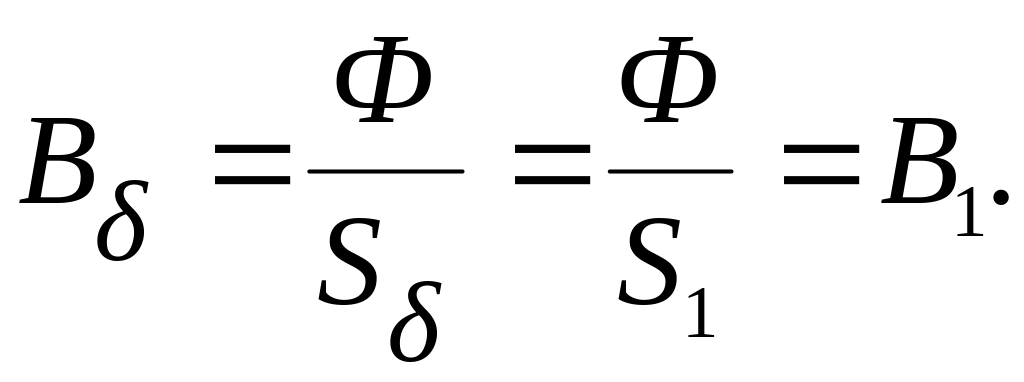
3) Значение напряжённости магнитного поля в ферромагнитных участках определяется по кривым намагничивания (рис. 2.7). Но в воздушном зазоре:

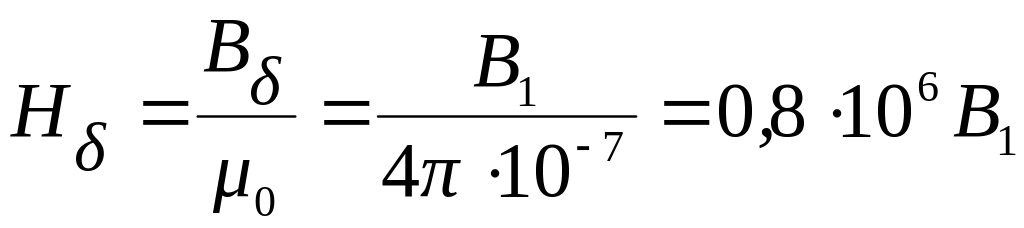
4) Для каждого участка определить падение магнитного напряжения:

5) Из второго закона Кирхгофа для магнитной цепи определим ток .

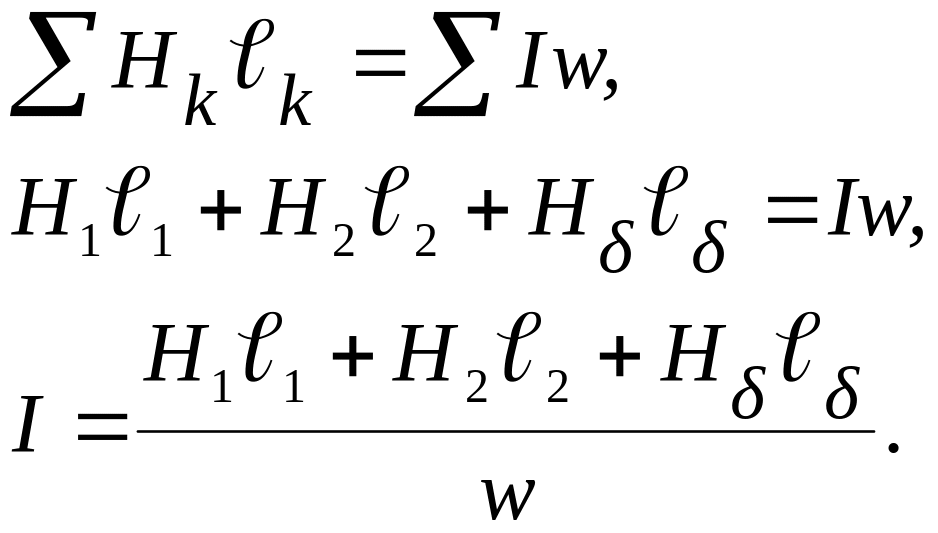
Обратная задача

Рассмотрим тот же пример (рис. 2.5), где также заданы геометрические размеры магнитной цепи: , число витков w и ток , кривые намагничивания

Определить магнитный поток .

Решение.

1 ) Разбить всю цепь на однородные участки и составить эквивалентную схему замещения (рис. 2.6). В данном случае, в конечном счёте, необходимо все три участка заменить эквивалентным нелинейным сопротивлением и найти его вебер-амперную характеристику ( ), а по ней – искомый магнитный поток , т.е. использовать метод преобразования нелинейной цепи (рис. 2.8).

П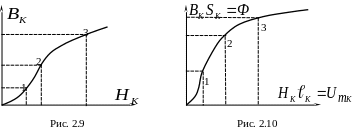 о известным кривым намагничивания (рис. 2.9) построить вебер-амперные характеристики путём умножения ординаты на и абсциссы на (рис 2.10).

Д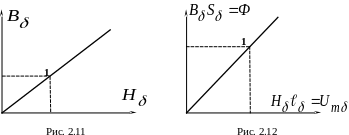 ля воздушного зазора вебер-амперную характеристику можно построить по одной точке, которую соединить с нулём прямой линией, т. к. – линейное сопротивление, (рис. 2.11 и рис. 2.12).

3 ) Совместить на одном графике вебер-амперные характеристики всех трёх участков и, задаваясь общим для данной цепи магнитным потоком , просуммировать магнитные напряжения каждого участка. По нескольким значениям магнитного потока построить результирующую вебер-амперную характеристику (рис. 2.13). По результирующей вебер-амперной характеристике определяем рабочую точку А, где выполняется второй закон Кирхгофа:

.

Отложив заданную намагничивающую силу , уравновешивающую сумму падений магнитных напряжений всей последовательной цепи, по рабочей точке А определяем магнитный поток .

Пример 2-3.

В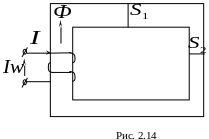 неразветвлённой магнитной цепи (рис. 2.14) два участка из одного материала, но сечение первого в два раза больше, чем сечение второго .

Сравнить магнитную индукцию этих участков и определить, какой из них ближе к насыщению.

Решение

В каждом участке один и тот же магнитный поток :

Тонкая часть сердечника с сечением ближе к насыщению, т. к. в два раза больше, чем .

Пример 2-4.

О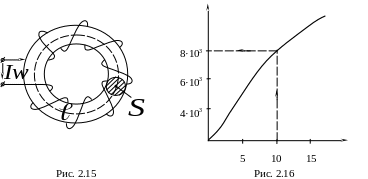 пределить индуктивность катушки с ферромагнитным сердечником (рис. 2.15), кривая намагничивания которого изображена на рис. 2.16, если =0,2 А, = 5 см², =20 см, = 1000 витков.

Решение.

Индуктивность определяем из известного соотношения:

где – потокосцепление.

Из второго закона Кирхгофа для магнитной цепи определим напряжённость магнитного поля .

.

По кривой намагничивания (рис. 2.16) определим магнитную индукцию =8·10³ = 0,8 .

Подсчитаем индуктивность: