1.4. Соединение трехфазной цепи треугольником

Чтобы соединить генератор в треугольник, нужно связать конец каждой фазы с началом следующей; в результате фазы генератора образуют замкнутый контур. При таком соединении симметричного генератора с отключенной нагрузкой ток внутри него не возникает, так как сумма ЭДС контура равна нулю. Соединив приемник также в треугольник (рис. 1.16), можно видеть, что фазные напряжения генератора и приемника одновременно являются и линейными, линейные же токи İ_A, İ_B, İ_C – отличны от фазных токов İ_AB, İ_BC, İ_CA.

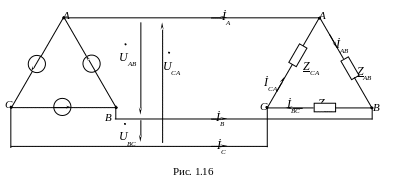
Для получения симметричных соотношений между линейными и фазными токами следует выбирать их положительные направления единообразно. Тогда по первому закону Кирхгофа

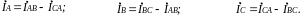
И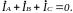 з полученных соотношений видно, что геометрическая сумма линейных токов равна нулю:

Линейные токи на векторной диаграмме образуют замкнутый треугольник.

При соединении трехфазной цепи треугольником можно выделить три частных случая.

1. Симметричная нагрузка (Z_AB=Z_BC=Z_CA).

Л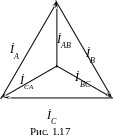 инейные токи на диаграмме образуют равносторонний треугольник (рис.1.17).

Достаточно определить ток одной фазы, в других фазах токи равны по величине, но имеют фазовый сдвиг +120º или -120º:

2) Несимметричная нагрузка, Z_пр=0, (Z_AB­­_­­­Z_BCZ_CA).

Если пренебречь сопротивлением проводов, напряжения генератора будут равны напряжениям приемника, фазы будут независимы друг от друга: всякое изменение сопротивления какой-либо фазы приемника вызовет изменение тока этой фазы и токов двух примыкающих к этой фазе линейных проводов, но никак не отразится на токах других фаз. Фазные токи определяются следующим образом:

3) Несимметричная нагрузка, Z_пр0, (Z_AB­­_­­­Z_BCZ_CA) .

Преобразуя треугольник сопротивлений приемника в эквивалентную звезду сопротивлений, задачу сводят к случаю соединения звездой (рис. 1.18).

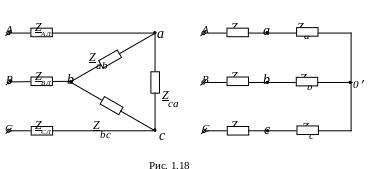
После определения токов звезды необходимо обратиться к исходному треугольнику, чтобы найти его фазные токи.

1.5. Построение векторных диаграмм для трехфазного треугольника

В любом случае построение диаграммы начинают с равностороннего треугольника линейных напряжений, который является одновременно треугольником фазных напряжений нагрузки, если пренебречь сопротивлением проводов линии. Затем откладывают фазные токи с соответствующим фазовым сдвигом по отношению к напряжению данной фазы. Переносят фазные токи на отдельный чертеж в одну точку и с учетом первого закона Кирхгофа получают линейные токи, замкнув концы фазных токов треугольником. Стрелку линейного тока направляют в сторону уменьшаемого фазного тока.

Пример 1-6.

Соединение треугольником при симметричной нагрузке Z_AB=Z_BC=Z_CA=Z=(10+j5,7) Ом и Z_пр=0, U_Л=220 В (рис. 1.16). Расчитать токи и построить векторную диаграмму напряжений и токов.

Решение

П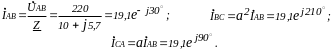 остроим равносторонний треугольник линейных напряжений. Определим ток каждой фазы (рис. 1.19):

Т ок каждой фазы на диаграмме откладываем под углом

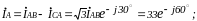
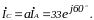
п 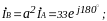о отношению к соответствующему фазному напряжению. Затем перенесем все фазные токи на отдельный чертеж в одну точку. С учетом первого закона Кирхгофа получаем линейные токи:

Л инейные токи образуют замкнутый равносторонний треугольник, причем направлен соответствующий линейный ток к соответствующему уменьшаемому фазному току.

Пример 1-7.

В цепи (рис. 1.20) R=X_L=X_C.

Построить векторную диаграмму напряжений и токов

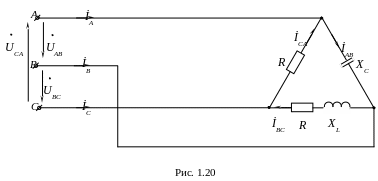
Решение

П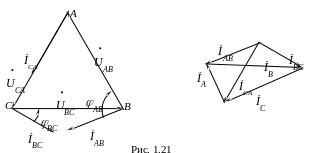 остроение диаграммы начинаем с равностороннего треугольника линейных напряжений U_AB, U_BC, U_CA (рис. 1.21).

П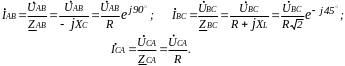 одсчитаем токи каждой фазы нагрузки и отложим векторы этих токов с учетом фазового сдвига по отношению к соответствующему напряжению фазы.

П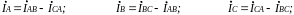 еренесем на отдельный чертеж фазные токи İ_AB, İ_BC, İ_CA в одну точку и, соединив их вершины, получим линейные токи

Стрелка линейного тока направлена в сторону уменьшаемого фазного тока.

Пример 1-8.

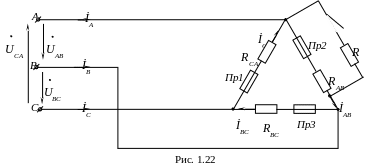
В схеме (рис. 1.22) R_AB=R_BC=R_CA=R . Как изменятся токи в цепи: 1) если замкнется рубильник; 2) если сгорит предохранитель Пр1 ?

Решение

1. П 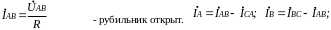ри замыкании рубильника сопротивление фазы АВ уменьшается в 2 раза:

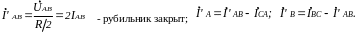
Токи остальных фаз не меняются. На векторной диаграмме (рис. 1.23) покажем токи до замыкания и после замыкания рубильника. Токи в линии А и В увеличиваются с увеличением тока фазы АВ, İ_C – не изменится.

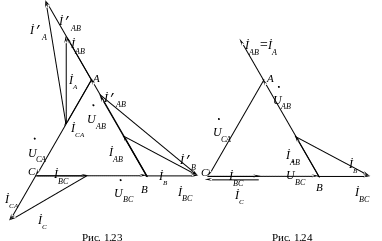
2. Если сгорит предохранитель Пр1, то ток фазы İ_CA=0, тогда линейные токи (рис. 1.24):

İ_A=İ_AB - уменьшится;

İ_B=İ_BC -İ_AB - не изменится;

İ_С= -İ_BC - уменьшится.

Пример 1-9.

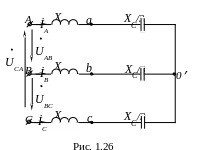
Найти линейные и фазные токи в цепи (рис. 1.25), если U_Л=220 В, X_L=5 Ом, X_C=3 Ом.

Решение

П реобразуем треугольник abc в эквивалентную звезду:

Определим эквивалентное сопротивление фазы преобразованной схемы

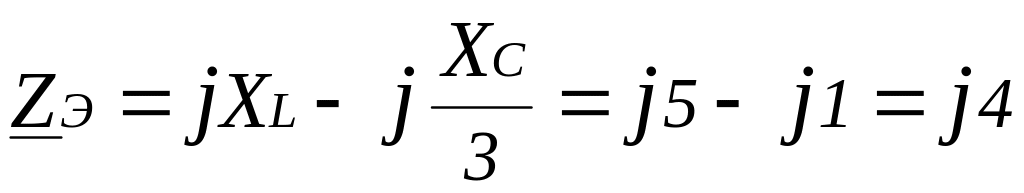( рис. 1.26):

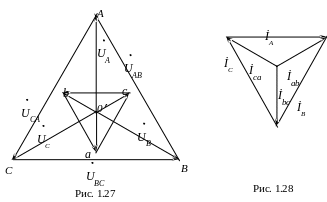
Расcчитаем линейные токи (рис. 1.26) и перенесем на диаграмму

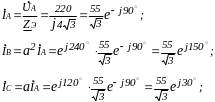( рис. 1.28).

Определим напряжения U_a0’, U_b0’, U_c0’ (рис. 1.26) и перенесем эти напряжения на векторную диаграмму (рис. 1.27).

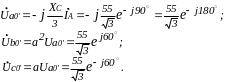
Рассчитаем напряжения треугольника abc (рис. 1.25) и перенесем на диаграмму (рис. 1.27).

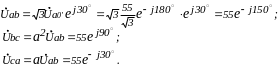
Р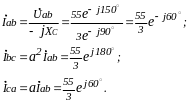 ассчитаем фазные токи исходной схемы (рис. 1.25) и перенесем их на диаграмму (рис. 1.28).