6.Решение системы n линейных уравнений с n неизвестными методом обратных матриц.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу , обратную матрице A: . Поскольку A = E и E∙X = X, то получаем решение матричного уравнения в виде X = B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = B.Для того чтобы решить  систему   линейных   уравнений   методом   обратной   матрицы, необходимо выполнить следующие действия:

• с 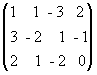формировать  матрицу  коэффициентов и вектор свободных членов заданной  системы ;

• решить  систему , представив вектор  неизвестных  как произведение  матрицы ,  обратной  к  матрице  системы , и вектора свободных членов

Пример:

Дана  система   уравнений :

Решаем :

A= ;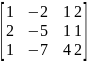

b=[2; -1; -2];

x=inv(A)*b %  Решение   системы  x=A^-1b

Результатом будет:

x =

0.5200

0.0800

1.6400

7. Система m линейных уравнений с n неизвестными. Метод Гаусса.

Система m линейных уравнений с n неизвестными (или, линейная система) в  линейной  алгебре — это  система   уравнений  вида

Здесь x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты  системы  — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij)  системы  обозначают номера  уравнения  (i) и  неизвестного  (j), при котором стоит этот коэффициент, соответственно^[1].

 Система  (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

 Система  (1) называется квадратной, если число  m   уравнений  равно числу  n   неизвестных .

Решение  системы  (1) — совокупность  n  чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в  систему  (1) обращает все её  уравнения  в тождества.

 Система  (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной  системы  вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная  система  вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если  уравнений  больше, чем  неизвестных , она называется переопределённой.

Метод Гаусса классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Таким образом, процесс решения системы линейных алгебраических уравнений по методу Гаусса состоит из двух этапов. Первый этап (прямой ход метода) – система приводится к треугольному виду.Второй этап (обратный ход) – неизвестные определяются последовательно, начиная с последнего неизвестного и кончая первым.

Пример 2.13. Решить систему уравнений методом Гаусса:

x +  y - 3z = 2,

3x - 2y +  z = - 1,

2x +  y - 2z = 0.

Решение. Выпишем расширенную матрицу данной системы

и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

 ~  ;

б) третью строку умножим на (-5) и прибавим к ней вторую:

.

В результате всех этих преобразований данная система приводится к треугольному виду:

                                                    x + y - 3z = 2,

                                                    -5y + 10z = -7,

                                                           - 10z = 13.

Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим  x = - 0,7.

8. Система линейных однородных уравнений.

Пусть дана система линейных однородных уравнений

Очевидно, что однородная система всегда совместна , она имеет нулевое (тривиальное) решение x1=x2=x3=...=xn=0.

Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т. е. r<n.

Необходимость:

Так как ранг не может превосходить размера матрицы, то, очевидно, r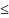 n. Пусть r=n. Тогда один из минеров размера nхn отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение:

Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то r<n.

Достаточность:

Пусть r<n. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т. е. имеет и ненулевые решения. Пусть дана однородная система n линейных уравнений с n неизвестными

Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель D был равен нулю, т. е. D=0.

Если система имеет ненулевые решения, то D=0. Ибо при D¹0 система имеет только единственное, нулевое решение. Если же D=0, то ранг r основной матрицы системы меньше числа неизвестных, т.е. r<n. И, значит, система имеет бесконечное множество (ненулевых) решений.