34.Первообразная функций и неопределенный интеграл. Свойства неопределенного интеграла.

В дифференциальном исчислении основной операцией является нахождение производной заданной функции. Сущность здесь заключается в установлении скорости изменения этой функции по сравнению с аргументом. Весьма часто, однако, приходится решать обратную задачу, когда по заданной скорости течения какого-либо процесса требуется восстановить сам этот процесс. В этом случае с математической точки зрения вопрос проводится к отысканию функции по ее производной. Эта операция, называемая интегрированием, является основной во второй половине математического анализа - интегральном исчислении.

     Пусть функция f(x), заданная в некотором промежутке^* [a, b], во всех его точках является производной функции F(x) , также заданной в [a, b]. Тогда эта последняя функция F(x) называется первообразной функцией для функции f(x) (в промежутке [a, b]).

     Имеет место

     Теорема 1. У всякой непрерывной на промежутке [a, b] функции имеется первообразная.

     Доказательство этой теоремы будет дано далее.

     Нетрудно видеть, что, если функция F(x) есть первообразная для f(x), то функция F(x) + C при любом постоянном C также является первообразной для f(x). В то же время никаких других первообразных, кроме функций вида F(x) + C, у f(x) уже быть не может. Действительно, если F₁(x) есть какая-то первообразная для f(x), то производная разности F₁(x) - F(x) будет всюду на [a, b] равняться нулю, а тогда сама разность есть величина постоянная, т. е.

F₁(x) - F(x) = C     и     F₁(x) = F(x) + C.

     Если F(x) есть первообразная функция для f(x), то функция двух аргументов x и C, равная F(x) + C, называется неопределенным интегралом функции f(x) и обозначается символом

     Таким образом, неопределенный интеграл какой-нибудь функции представляет собой общий вид первообразных функций для этой функции. Величина C, входящая в определение неопределенного интеграла, называется "произвольной постоянной". Придавая ей то или иное закрепленное значение, можем получить из неопределенного интеграла любую первообразную.

     Легко понять, что из самого определения понятия интеграла вытекает следующее утверждение:

     Теорема 2. Производная неопределенного интеграла равна подинтегральной функции, т. е.

35.Таблица интегралов. Метод подстановки и интегрирование по частям.

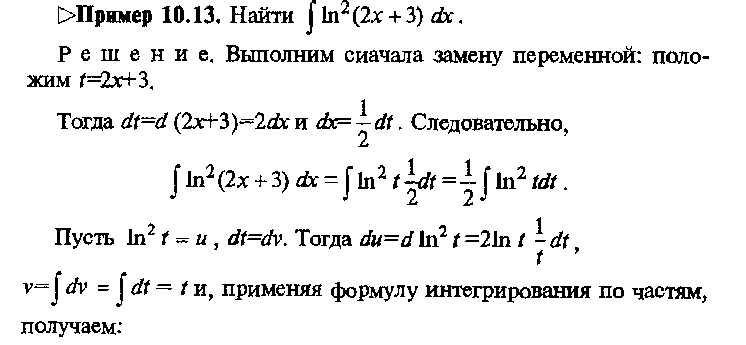
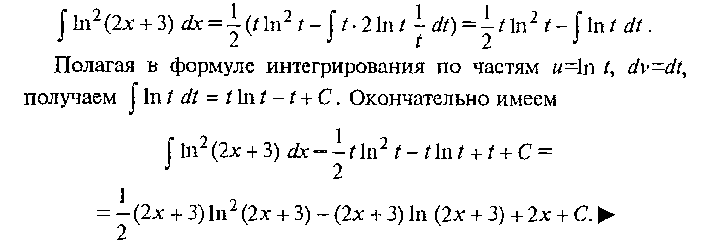
36.Интегрирование простейших рациональных выражений.

37.Определенный интеграл и его свойства.

38.Несобственные интегралы.

39.Вычисление площадей плоских фигур, объемов тел вращения и длин дуг кривой.

ТРЕУГОЛЬНИК

	S =	bh	;	S =	abc
		2			2

S =

√

p(p−a)(p−b)(p−c)

S = pr

p = 1/2 (a + b + c)

П АРАЛЛЕЛОГРАММ

S = bh

РОМБ

	S =	Dd
		2

ПРЯМОУГОЛЬНИК

S = ab =

a √

d2 − a2

= b √

d2 − b2

ТРАПЕЦИЯ

S =	a + b	h
	2

КРУГ

S = πr2 =	πd2
	4
C = 2πr = πd

КОЛЬЦО

S = π (R2 − r2)

Вычисление   объемов   тел   вращения 

Постановка задачи. Вычислить  объем   тела , образованного  вращением  области, ограниченного графиками функций   и   и, возможно, прямыми   и  , вокруг оси . План решения

Объем   тела , образованного  вращением  области, ограниченной кривыми   и   и прямыми   и  , где  , т.е. области, определяемой системой неравенств вычисляется по формуле . (1)

1. Определяем область D. Если неравенства, определяющие область D, неизвестны, т.е. неизвестны a и b и/или неизвестно, какая из функций   и  больше другой на отрезке  , то выполняем следующие операции:

а) находим a и b как абсциссы точек пересечения графиков функций   и   , т.е. решаем уравнение ;

б) исследуем знак разности   на отрезке  . Для этого достаточно вычислить значение   в какой-нибудь точке из  . Если оно положительно, то   и, следовательно,   и  . Если оно отрицательно, то   и, следовательно   и .

2. Вычисляем  объем  по формуле (1).

Замечание 1. Иногда бывает полезным построить график области D и фигуры  вращения .

Замечание 2. Аналогично решается задача, если  тело  образовано  вращением  области вокруг оси Oy.

Длина дуги пространственной и плоской кривой, заданной параметрически Если пространственная кривая задана параметрически , то длина дуги вычисляется по формуле: Аналогично для плоской кривой: Длина дуги плоской кривой, заданной явно Если функция у = f(x) непрерывно дифференцируема на отрезке [а, b], тогда длина дуги соответствующей кривой имеет вид: Длина дуги плоской кривой, заданной в полярных координатах  - непрерывно дифференцируемая на отрезке [ ,  ] функция, определяющая плоскую кривую;          .40.Дифференциальные уравнения. Основные понятия.

Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например,   не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.

Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.

Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y'(x),y''(x),...,yⁿ(x) до порядкаn включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.

Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.

Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функциивремени.

обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида

 или  ,

где   — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной времени  , штрих означает дифференцирование по  . Число   называется порядком дифференциального уравнения.

Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:

,

где   — независимые переменные, а   — функция этих переменных.