22. Смешанное произведение векторов и его свойства.

Определение 6.4. Смешанным произведением векторов а, b и с называется результат скалярного умножения векторного произведения [ab] на вектор с. Обозначение: abc = [ab]c.

Свойства смешанного произведения:

1) Смешанное произведение [ab]c равно объему параллелепипеда, построенного на приведенных к общему началу векторах a,b,c, если они образуют правую тройку, или числу, противоположному этому объему, если abc – левая тройка. Если a,b и с компланарны, то [ab]c = 0.

Доказательство: а) Если a,b и с компланарны, то вектор [ab] ортогонален плоскости векторов а и b, и, следовательно, [ab] c. Поэтому [ab]c = 0. в) Если a,b,c не компланарны, [ab]c = |[ab]||c| = S·|c|cosφ, где φ – угол между с и [ab]. Тогда |c|cosφ – высота рассматриваемого параллелепипеда. Таким образом, [ab]c = V, где выбор знака зависит от величины угла между с и [ab]. Утверждение доказано.

Следствие: [ab]c = a[bc]. Действительно, обе части равенства представляют объем одного и того же пераллелепипеда. Поэтому положение векторных скобок в смешанном произведении не важно, и в его обозначении скобки не ставятся : abc.

2) Если a = {X_a, Y_a, Z_a}, b = {X_b, Y_b, Z_b}, c = {X_c, Y_c, Z_c}, то abc = .

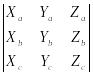Доказательство: Используя координатную запись скалярного и векторного произведения, запишем: [ab]c = (Y_aZ_b – Y_bZ_a)X_c + (X_bZ_a – X_aZ_b)Y_c + (X_aY_b – X_bY_a)Z_c = .

24. Двойное векторное произведение.

Формула Лагранжа: для двойного векторного произведения справедлива формула Лагранжа, которую можно запомнить по мнемоническому правилу «бац минус цаб».

Док-во: Выберем правый ортонормированный базис так, чтобы

, , . Тогда

, и

Таким образом,

Тождество Якоби: для двойного векторного произведения выполняется тождество Якоби , которое доказывается раскрытием скобок по формуле Лагранжа

25. Плоскость в пространстве (основные виды уравнений).

Ур-ием (нер-вом) фигуры называется ур-ие (нер-во удовл. следующим двум условиям:

1) если точка принадлежит фигуре, то её координаты удовл. данному ур-ию (нер-ву).

2) если координата некоторой точки удовл. ур-ию (нер-ву), то точка принадлежит фигуре.

Плоскость.

1) Общее ур-ие плоскости

Ax+By+Cz+D=0

2) Ур-ие плоскости проходящей через точку x0 , y0, z0 , перпендикулярно вектору n с коорд. (A,B,C,)

A (x-x0 )+B(y-y0 )+C(z-z0 )=0

3) Ур-ие плоскости, прох. через 3 точки

Даны М1 М2 М3. M (x,y,z) произвольная точка в пл-ти. M1М, М1M2, М1M3 – компланарны.

4) Ур-ие плоскости в отрезках.

О А=a; OB=b; OC=c; A=(a;0;0); B=(0;b;0); C=(0;0;c);

26. Нормальное уравнение плоскости. Расстояние от точки до плоскости.

5) Нормальное (нормированное) уравнение плоскости .

В векторной форме: , где - единичный вектор, - расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель (знаки и противоположны).

Расстояние от точки до плоскости - это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость. Расстояние от точки , до плоскости, заданной уравнением , вычисляется по формуле: .