8. Решение системы линейных алгебраических уравнений методом Гаусса.

Суть метода заключается в последовательном исключении неизвестных. Рассмотрим систему линейных уравнений: 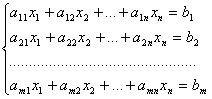Разделим обе части 1–го уравнения на a11 <> 0, затем: 1) умножим на а21 и вычтем из второго уравнения 2) умножим на а31 и вычтем из третьего уравнения и т.д. Получим: 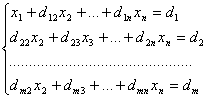, где d1j = a1j/a11, j = 2, 3, …, n+1. dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1. Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.

Допускаются следующие элементарные преобразования:

1)Перестановка строк расширенной матрицы.

2)Умножение i-й строки расширенной матрицы на число альфа, не равное нулю.

3)Прибавление к i-й строке расширенной матрицы j-ю строку умноженную на заданное число альфа.

рассмотрим некоторые ситуации:

( 0 0 0 ... 0 I bi ) - нет решений

две одинаковые строчки. - одну из них можно вычеркнуть.

если в строчке стоят одни нули, то мы её вычёркиваем.

9. Линейное пространство. Примеры линейных пространств.

Линейное, или векторное пространство над полем P - это непустое множество L, на котором введены операции сложения, то есть каждой паре элементов множества ставится в соответствие элемент того же множества, обозначаемый и умножения на скаляр (то есть элемент поля P), то есть любому элементу и любому элементу ставится в соответствие элемент из , обозначаемый .

При этом удовлетворяются следующие условия:

, для любых (коммутативность сложения);

, для любых (ассоциативность сложения);

существует такой элемент , что для любого (существование нейтрального элемента относительно сложения), в частности L не пусто;

для любого существует такой элемент , что (существование противоположного элемента).

(ассоциативность умножения на скаляр);

(умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).

(дистрибутивность умножения на вектор относительно сложения скаляров);

(дистрибутивность умножения на скаляр относительно сложения векторов).

Элементы множества L называют векторами, а элементы поля P - скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.

10. Линейная зависимость и независимость векторов.

Говорят, что вектор линейного пространства L линейно выражается через векторы , если его можно представить в виде линейной комбинации этих элементов , т.е. представить в виде .

Определение. Система векторов произвольного линейного пространства линейно независима если из равенства следует равенство нулю всех коэффициентов .

Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой.

Теорема. Система векторов произвольного линейного пространства линейно зависима тогда и только тогда, когда хотя бы один вектор системы векторов линейно выражается через остальные векторы системы.

Система векторов называется линейно зависимой (л.з.) если существуют числа , хотя бы одно из которых отлично от нуля, такие что . Если же это равенство возможно только при , то система векторов называется линейно независимой (л.н.з.).

11. Размерность линейного пространства. Базис, координаты.

Определение. Число k называется размерностью линейного пространства L, если в L существует система из k линейно независимых векторов, а любые k+1 вектора — линейно зависимы; обозначаем dim L=k.

Определение. Совокупность линейно независимых векторов линейного пространства L называется базисом этого пространства, если любой вектор из L линейно выражается через векторы , т.е. для любого x из L существуют такие числа что .

Если , то разложение вектора по базису становится суммой слагаемых: В этом случае говорят, что вектор разложен по базису , а числа называются координатами вектора в этом базисе.