11.2.2 Алгебраические критерии устойчивости

Для решения вопроса об устойчивости или неустойчивости невозмущенного движения можно не определять корни характеристического уравнения, а лишь определить знак вещественной части всех корней, которые для устойчивого дижения должны быть строго отрицательными.

Косвенные признаки, по которым можно судить о знаке вещественной части корней характеристического уравнения линейных систем с постоянными коэффициентами, минуя вычисление самих корней, называются критериями устойчивости. Они подразделяются на алгебраические и частотные.

Алгебраические критерии позволяют судить об устойчивости и неустойчивости систем по коэффициентам характеристического уравнения. Имеются различные формы критериев. Наибольшее применение получили критерии Гурвица и Рауса.

Пусть характеристическое уравнение n-ой степени имеет вид

(11.15)

в котором все коэффициенты a_k – вещественные числа, а a_n > 0. Построим из коэффициентов матрицу Гурвица (n ´ n)

D1		an-1	an	0	0	·	0
D2		an-3	an-2	an-1	an	·	0
D3		an-5	an-4	an-3	an-2	·	0
D4		an-7	an-6	an-5	an-4	·	0
·		·	·	·	·	·	0
Dn		0	0	0	0	0	a0

Теорема Гурвица. Для того, чтобы все корни алгебраического уравнения (11.15) имели отрицательные вещественные части, необходимо и достаточно, чтобы все главные диагональные миноры матрицы Гурвица были положительны.

В частности для уравнения четвёртой степени

() (11.16)

должны выполняться неравенства: ; ;

; .

Равносильными для уравнения 4-ой степени являются условия Рауса-Гурвица, которые имеют вид: .

Лекция 17.

11.2.3 Решение линейных дифференциальных уравнений с постоянными коэффициентами операторным методом

Сущность этого метода состоит в том, что посредством интегрального преобразования от систем линейных дифференциальных уравнений переходят к вспомогательной системе алгебраических уравнений. Затем находят решение вспомогательной системы, а из него при помощи обратного преобразования получают решение исходной системы дифференциальных уравнений.

В качестве интегрального преобразования чаще всего используют преобразование Лапласа:

, (11.17)

где параметр p – некоторое комплексное число, y(t) – кусочно-непрерывная и ограниченная функция независимой переменной t, называемая оригиналом; Y(p) – изображение функции y(t). Помимо прямого преобразования существует обратное преобразование Лапласа, позволяющее по изображению Y(p) находить оригинал y(t). Сокращённое обозначение обратного преобразования: .

В курсах операционного исчисления приводят таблицы прямого и обратного пре-

образования основных функций.

Математическая операция	Оригинал	Изображение
Исходное преобразование	y(t)	Y(p)
Сложение оригинала
Умножение на постоянное число	аy(t)	аY(p)
Дифференцирование	dy/dt частн. случай: при y0=0	pY(p)-y0 pY(p)
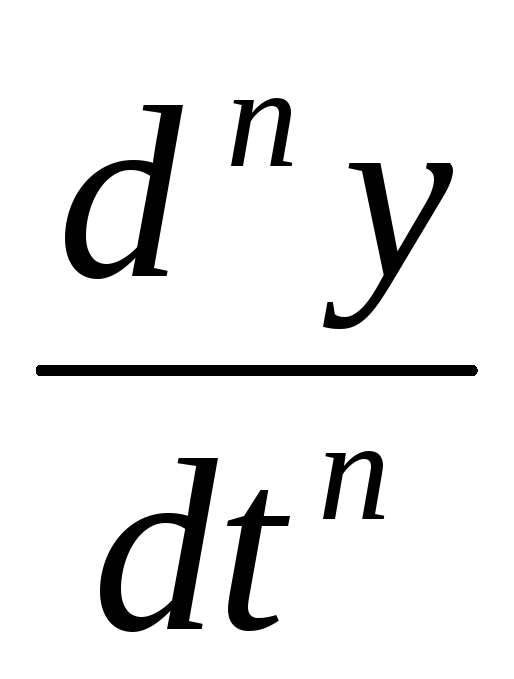
n– кратное дифференцирование		PnY(p)-[pn-1y0+ +pn-2+…+]
Интегрирование
Сдвиг оригинала на (смещённый аргумент )	y(t -)

При анализе возмущенного движения ЛА часто возникает необходимость определить предельные значения решения дифференциального уравнения по виду этого уравнения, не решая его. Например, надо оценить поведение функции y(t) при t 0 или при t, при условии, что система устойчива. Эту задачу решают при помощи следующих теорем о предельном переходе в преобразованиях Лапласа:

1. Если существует предел функции , то

(11.18)

2. Если существует предел функции , то

(11.19)