Геометрический смысл плохо обусловленных и хорошо обусловленных матриц
Рассмотрим систему уравнений
При плохой обусловленности матрицы эти прямые почти параллельны, поэтому любое небольшое возмущение в правой части сказывается на определении точного решения.
Для хорошо обусловленных систем прямые проходят под большим углом, точность решения – высокая.
11. Задачи приближения и интерполяции функций и эмпирических данных.
Задачей приближения или аппроксимации называется задача построения функции, принимающей в заданных точках заданные значения.
Значения функции в заданных точках могут быть представлены в табличной форме и получаются или из экспериментов, или посредством расчета некоторой сложной функции.
Значения функции задаются в системе
точек
– узлы интерполяции.
Каждому узлу интерполяции соответствуют
значения функции
.
Точное значение функции
неизвестно, либо ее вычисление сложно.
Задача заключается в нахождении оценки
(аппроксимации) интерполирующей функции
.
Форма аппроксимирующей функции известна,
не известны параметры
.
Задача заключается в нахождении этих
параметров из условия, что значение
аппроксимирующей функции в узлах
интерполяции совпадают с известными
значениями
:
В общем случае – это система нелинейных
уравнений относительно
.
Для того, чтобы она имела решения
необходимо, чтобы число уравнений было
равно числу неизвестных
.
В качестве аппроксимирующей функции используется линейная комбинация линейно-независимых функций, т.е., как правило, аппроксимирующая функция:
.
Система функций
,
с помощью которой представляется
аппроксимирующая функция, называется
базисной функцией (БСФ) или базисом.
В качестве БСФ используются:
1) степенные многочлены:
;
2) тригонометрическая система функций:
;
3) ортогональные между собой многочлены
Задача интерполяции заключается в
нахождении значений функции
при
.
???12. Задача интерполяции алгебраическим многочленом с простыми узлами. Формулы Лагранжа и Ньютона. Разделенные разности.
В качестве интерполяционных многочленов может быть использован многочлен Лагранжа, который может быть записан:
Формула Ньютона:
Однако, применение этих формул при использовании интерполяционных многочленов высокого порядка (чем больше порядок многочлена, тем большую точность можно ожидать) сопряжено с большим объемом предварительных вычислений, а также с тем, что эти методы трудно обобщаются на случай функции нескольких переменных.
Более простое решение задач численного дифференцирования достигается с помощью метода неопределенных коэффициентов.
Короткая форма интерполяционной формулы Ньютона для случая равноудаленных узлов:
Рассмотрим последовательность значений функции в узлах интерполяции, она называется разделенной разностью нулевого порядка.
Разделенные разности первого порядка определяется по формуле:
В общем случае:
Разделенная разность второго порядка.
– это разделенная разность первого
порядка
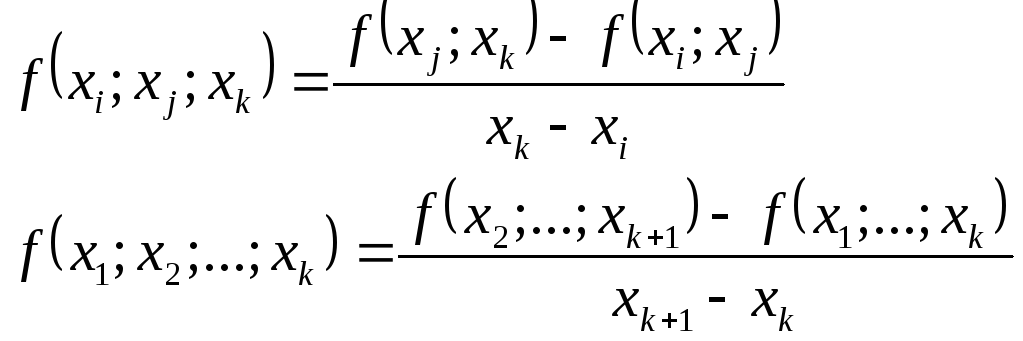
Таблица разделенных разностей
Интерполяционная формула Ньютона с помощью разделенных разностей запишется:
При вычислении многочлена по интерполяционным формулам необходимо учитывать вычислительную сложность алгоритма.
Существуют различные способы вычисления многочлена, которые отличаются по своей вычислительной сложности, т.е. по числу вычислительных операций.