23. Интегрирование быстро осциллирующих функций. Интегрирование функций на больших интервалах изменения аргумента.

24. Тригонометрическая интерполяция и дискретное преобразование Фурье.

Лемма 1

Если , то .

Доказательство:

Лемма 2

Учитывая лемму 1, значения функции на сетке узлов можно задать с помощью выражения

В силу периодичности функции: .

Пусть определено скалярное произведение функций f и g:

Скалярное произведение функций f и g задается как произведение выборок этих в точках .

Пусть – комплексная экспонента в узлах .

Рассмотрим скалярное произведение функций:

Сумма представляет собой геометрическую прогрессию.

– целое число

Отсюда следует, что комплексные экспоненты на узлах сетки являются ортонормальными функциями.

Любой периодический сигнал может быть представлен в форме ряда Фурье.

При рассмотрении непериодического сигнала на интервале , функция продолжается периодическим образом вне этого интервала. Вводится функция

В этом случае непериодическая на интервале функция может быть представлена рядом Фурье периодической функцией .

Интервал посредством преобразования аргумента может быть приведен к интервалу .

Интервал будет считаться интервалом .

Ряд Фурье непрерывной функции на интервале :

Значение функция на сетке узлов, расположенных с шагом записывается:

Узлы с шагом делят интервал на N подинтервалов

В силу периодичности функции: : .

Значения функции . Это выражение называется дискретным рядом Фурье.

Значения дискретного ряда Фурье совпадают со значениями функции на сетке узлов .

Если заменить дискретным рядом Фурье дискретную переменную на непрерывную переменную, то мы получим функцию , которую можно назвать тригонометрической интерполяционной формулой, функцией , заданной на сетке узлов.

Значения интерполяционной формулы на сетке узлов совпадают со значениями функции : . Между узлами сетки эти функции значительно отличаются друг от друга.

Т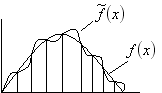очность приближения интерполяционной формулы зависит от величины шага интерполяции или, по другому, периода дискретизации функции.

Вычисления коэффициентов дискретного ряда Фурье через коэффициенты непрерывного ряда Фурье является дискретной процедурой, т.к. сумма представляет бесконечный ряд.

Более рациональным является определение коэффициентов ряда Фурье, основанное ортогональности экспоненциальных функций.

Отображение множества значений функции на множество коэффициентов дискретного ряда Фурье называется прямым дискретным преобразованием Фурье, а его коэффициенты: .

Отображение коэффициентов дискретного ряда Фурье на значения функции в узлах сетки называется обратным дискретным преобразованием Фурье: .

Значения отображения: .

25. Быстрое преобразование Фурье.

С целью умножения числа операций при вычислении дискретного преобразования Фурье (ДПФ) используется быстрое преобразование Фурье (БПФ).

Идея метода БПФ основывается на том, что число N выбирается таким, чтобы оно представляло собой произведение некоторого числа простых чисел: .

Путем преобразования выражений БПФ число операций сокращается:

На практике принимается: , ,