28. Алгоритм qr-разложения. Ортогональные матрицы и матрицы плоского вращения.
модулю 1.
Это следует из неравенства Коши-Шварца:
Сохранение углов между векторами следует из равенства:
QR-разложение может быть осуществлено методами вращения и отражения.
Рассмотрим вращение вектора
на плоскости.
Матрица вращения задается в виде:
,
– угол вращения.
Свойство ортогональной матрицы – сохранение угла между векторами.
Видно, что матрица вращения – ортогональная матрица:
Если принять, что
или
,
то
.
Рассмотрим систему линейных алгебраических уравнений второго порядка:
Найдем матрицу Q такую,
что
,
где
Рассмотрим систему уравнений с матрицей
.
Плоской матрицей вращения называется матрица, имеющая вид:
Можно подтвердить, что матица Q является ортогональной матрицей с определителем, равным 1.
Применение указанной матрицы к i-му
столбцу матрицы A:
,
дает вектор
,
имеющий в j-ой позиции 0.
(Верхний индекс обозначает номер
вектора).
Применяя к исходной матрице указанные плоские матрицы вращения получим матрицу:
С помощью указанных матриц вращения все элементы матрицы R ниже главной диагонали становятся равными нулю.
Для исключения соответствующих элементов, коэффициенты c и s определяются выражениями:
Произведение ортогональных матриц является ортогональной матрицей.
Чтобы решить задачу, матрица A
дополняется матрицей
,
матрица A является
произвольной.
Учитывая, что ортогональное преобразование вектора невязки:
второе слагаемое не зависит от
коэффициентов многочлена, линейное
значение первого слагаемого сводится
к решению системы уравнений:
,
где R – верхняя
треугольная матрица.
Решение задачи наименьших квадратов
при
,
сводится к задаче решения системы
алгебраических уравнений с верхней
треугольной матрицей:
Чтобы применить метод QR-разложения к решению задачи наименьших квадратов, нужно привести матрицу A к квадратной форме:
матрица B – произвольная.
Исходное уравнение:
Матрица
является квадратной
.
К этой системе можно применить метод
QR-разложения.
Применяя метод вращения, уравнение
записывается:
,
размерность вектора
,
размерность вектора
,
– ортогональная матрица,
– верхняя треугольная матрица.
Разобьем матрицу R на блоки:
Умножая матрицу R
справа на
можем записать:
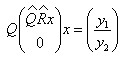
невязка (ошибка)
От неизвестных параметров зависит только первое слагаемое нормы невязки.
Минимальное значение этого слагаемого,
если матрица A
максимальный размер, определяется из
уравнения:
.
Таким образом, задача наименьших квадратов решается в два этапа.
На первом этапе осуществляется
QR-разложение расширенной
матрицы и определяются ее подматрицы
и
.
На втором этапе решается задача решения системы линейных алгебраических уравнений, матрица которой представлена в QR форме.
Матрица Q является ортогональной матрицей, т.е. матрицей, транспонирование которой совпадает с обратной матрицей.
Матрица R – верхняя треугольная матрица, решение которой осуществляется методом обратной подстановки.