
- •1. Источники и виды погрешностей. Абсолютная и относительная погрешности. Вычислительная погрешность и погрешность функции.
- •3. Решение систем линейных алгебраических уравнений. Правило Крамера и обратная матрица. Вычислительная сложность.
- •4. Решение систем линейных уравнений. Метод исключения Гаусса с верхней и нижней треугольной матрицами. Методы прямой и обратной подстановки. Решение линейных систем алгебраических уравнений
- •Метод исключения Гаусса без перестановки строк
- •5. Решение систем линейных уравнений с симметричными и положительно определенными матрицами. Разложение Холесского с внутренним произведением.
- •6. Разложение Холесского с внешним произведением и с поблочным вычислением матриц.
- •Доказательство теоремы Халецкого
- •7. Метод исключения Гаусса и lu-разложение. Понятие эквивалентности систем уравнений, понятие и состав элементарных операций.
- •8. Алгоритм исключения Гаусса без перестановки строк. Lu- и ldv-разложения.
- •9. Алгоритм исключения Гаусса при наличии вырожденных главных подматриц. Алгоритм с перестановкой строк или с выбором главного элемента.
- •10. Свойства и определения матричных и векторных норм. Теорема Коши – Шварца. Число обусловленности системы линейных уравнений. Геометрический смысл числа обусловленности. Матричная норма
- •Геометрический смысл плохо обусловленных и хорошо обусловленных матриц
- •11. Задачи приближения и интерполяции функций и эмпирических данных.
- •13. Формулы численного дифференцирования интерполяционным методом.
- •14. Формулы численного дифференцирования методом неопределенных коэффициентов.
- •15. Наиболее распространенные формулы численного дифференцирования.
- •16. Задачи и методы численного интегрирования. Квадратурные формулы.
- •Элементарные квадратурные формулы, полученные методом интерполяции
- •17. Численное интегрирование интерполяционными методами.
- •18. Численное интегрирование методом неопределенных коэффициентов.
- •Частные случаи
- •19. Квадратурные формулы Ньютона – Котеса.
- •20. Формулы прямоугольника, трапеций и Симпсона.
- •21. Ортогональные и ортонормальные системы функций и многочленов. Скалярное произведение. Ортогонализация произвольной системы линейно независимых функций. Формула Грама – Шмидта.
- •22. Квадратурные формулы Гаусса. Наиболее распространенные формулы.
- •23. Интегрирование быстро осциллирующих функций. Интегрирование функций на больших интервалах изменения аргумента.
- •24. Тригонометрическая интерполяция и дискретное преобразование Фурье.
- •25. Быстрое преобразование Фурье.
- •26. Задача наименьших квадратов. Прямой метод решения.
- •27. Задача наименьших квадратов. Решение методом qr-разложения.
- •28. Алгоритм qr-разложения. Ортогональные матрицы и матрицы плоского вращения.
- •29. Задача численного решения обыкновенных дифференциальных уравнений. Задача Коши и граничные задачи.
- •30. Решение задачи Коши с помощью формулы Тейлора.
- •31. Методы Рунге – Кутта. Формулы Эйлера и Адамса.
- •32.Конечно-разностные методы решения задачи Коши.
- •33. Явные формулы Адамса.
- •34. Решение задачи Коши методом неопределенных коэффициентов.
- •35. Решение систем обыкновенных дифференциальных уравнений методом Эйлера.
- •36. Определение градиента функции нескольких переменных.
- •Метод градиента
- •37. Матрица Якоби системы функций нескольких переменных.
- •38. Решение нелинейных уравнений методом простой итерации.
- •39. Решение нелинейных уравнений методом Ньютона.
- •46. Необходимые и достаточные условия минимума и максимума функции многих переменных. Необходимые и достаточные условия экстремума функции нескольких (двух) переменных
- •47. Форма функции многих переменных в окрестности точки седла.
- •48. Градиентный метод минимизации функции многих переменных.
- •49. Минимизация функции многих переменных методом Ньютона.
- •Применительно к задачам оптимизации
- •50. Формула и множители Лагранжа в задаче оптимизации
- •Описание метода
- •51. Производная по направлению и возможное направление спуска.
- •52. Обратные и некорректные задачи.
47. Форма функции многих переменных в окрестности точки седла.


Седловая точка функции (обозначена красным) , седловая точка точка центр "восьмерки".
Седловая точка в математическом анализе — такая точка из области определения функции, которая является стационарной для данной функции, однако не является её локальным экстремумом. В такой точке, если рассматривается функция двух переменных, образованная графиком функции поверхность обычно напоминает по форме седло или горный перевал - выпуклая в одном направлении и вогнутая в другом. На карте высот седловая точка может быть в общем случае обнаружена в месте пересечения изолиний. Например, два холма, между которыми находится высокий перевал, образуют седловую точку в вершине этого перевала: на карте высот это будет выглядеть как центр "восьмерки", образованной соответствующими изолиниями.
Седловая точка в математическом анализе
Проверить, является
ли данная стационарная точка функции F(x,y)
двух переменных седловой, можно,
вычислив матрицу
Гессе функции
в этой точке: если гессиан будет
неопределенной квадратичной
формой,
то данная точка - седловая. Например,
составив матрицу Гессе функции z = x2 − y2 в
стационарной точке (0,0) получим
матрицу:![]()
которая является неопределенной. Поэтому, точка (0,0) данной функции - седловая. Однако вышеприведенный критерий предоставляет только достаточное условие наличия седловой точки. Например, (0,0) является седловой точкой функции z = x4 − y4, но матрица Гессе в данном случае будет нулевой матрицей, которую, по определению, нельзя назвать неопределенной.
В общем случае, седловой точкой гладкой функции (чей график изображает кривую, поверхность или гиперповерхность) называется такая стационарная точка, в окрестности которой данная кривая/поверхность/гиперповерхность не лежит полностью на одной стороне касательного пространства в данной точке.
В
случае функции одной переменной, седловая
точка - такая точка, которая одновременно
и стационарная точка, и точка
перегиба (точка
перегиба не является локальным
экстремумом).Термин
«седловая точка» также используется
для обозначения элемента матрицы,
который является наименьшим элементом
в своем ряду и наибольшим в своем столбце
(или же наоборот, то есть наибольший в
ряду и наименьший в столбцеНапример,
матрица![]() имеет
одну седловую точку — «4» в первом
ряду третьем столбце меньше, чем элементы
в первом ряду матрицы («5», «6», «5»), и
больше, чем элементы в третьем столбце
(«3», «-2»).
имеет
одну седловую точку — «4» в первом
ряду третьем столбце меньше, чем элементы
в первом ряду матрицы («5», «6», «5»), и
больше, чем элементы в третьем столбце
(«3», «-2»).
![]() Матрица
содержит
4 седловых точки — «2» в первом и
втором ряду, первом и четвёртом столбце.
Данный пример показывает, что матрица
может иметь любое количество седловых
точек. Так, в матрице, состоящей из одного
и того же числа, все элементы являются
седловыми.
Матрица
содержит
4 седловых точки — «2» в первом и
втором ряду, первом и четвёртом столбце.
Данный пример показывает, что матрица
может иметь любое количество седловых
точек. Так, в матрице, состоящей из одного
и того же числа, все элементы являются
седловыми.
![]() Матрица
не
имеет седловой точки.
Матрица
не
имеет седловой точки.
48. Градиентный метод минимизации функции многих переменных.
Градиентный спуск — метод нахождения локального минимума (максимума) функции с помощью движения вдоль градиента. Для минимизации функции в направлении градиента используются методы одномерной оптимизации, например, метод золотого сечения. Также можно искать не наилучшую точку в направлении градиента, а какую-либо лучше текущей.
Сходимость метода градиентного спуска зависит от отношения максимального и минимального собственных чисел матрицы Гессе в окрестности минимума (максимума). Чем больше это отношение, тем хуже сходимость метода.
Описание
Иллюстрация последовательных приближений к точке экстремума в направлении наискорейшего спуска (красн.) в случае дробного шага. Синим отмечены линии уровня.

Пусть целевая функция имеет вид:
-
 .
. -
И задача оптимизации задана следующим образом:
-
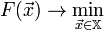
-
Основная идея метода заключается в том, чтобы идти в направлении наискорейшего спуска, а это направление задаётся антиградиентом
 :
: -

где λ[j] выбирается
-
постоянной, в этом случае метод может расходиться;
-
дробным шагом, т.е. длина шага в процессе спуска делится на некое число;
-
наискорейшим спуском:
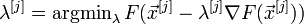
Алгоритм
Задают
начальное приближение и точность
расчёта ![]()
-
Рассчитывают
 ,
где
,
где 
-
Проверяют условие остановки:
-
Если
 или
или  (выбирают
одно из условий), то j = j +
1 и переход к
шагу 2.
(выбирают
одно из условий), то j = j +
1 и переход к
шагу 2. -
Иначе
 и
останов.
и
останов.
