
- •Производная функции. Дифференцирование суммы, разности, произведения и частного двух функций. Геометрический смысл производной функции.
- •Дифференциал функции, его свойства.
- •Дифференцирование элементарных функций. Табличные производные.
- •Неопределённый интеграл, его свойства.
- •Методы интегрирования: метод непосредственного интегрирования и метод разложения. Табличные интегралы.
- •Метод интегрирования по частям и метод замены переменной под знаком интеграла.
- •Понятие матрицы. Операции над матрицами, их свойства.
- •Квадратная матрица. Треугольная, диагональная, единичная матрицы. Степень квадратной матрицы. Матричный многочлен.
- •Определитель квадратной матрицы. Вычисление определителей второго и третьего порядков.
- •Свойства определителей.
- •Общие способы вычисления определителей.
- •Ранг матрицы, его свойства. Методы нахождения ранга матрицы.
- •Обратная матрица. Теорема о существовании обратной матрицы. Методы нахождения обратной матрицы.
- •Собственные значения матрицы. Собственные и присоединённые векторы матрицы.
- •Комплексные числа, их геометрическая интерпретация.
- •Корень n-ой степени из комплексного числа. Логарифм и степень комплексного числа.
- •Правило Крамера. Решение линейных систем алгебраических уравнений.
- •Системы линейных алгебраических уравнений. Общие понятия. Теорема Кронекера-Капелли.
- •Однородные и неоднородные системы линейных алгебраических уравнений. Теоремы о существовании решений. Структура общего решения.
- •Системы координат на плоскости.
- •Прямая на плоскости. Различные уравнения прямой на плоскости
- •Условия пересечения, параллельности, совпадения и перпендикулярности двух прямых на плоскости. Определение угла между двумя прямыми.
- •Уравнение кривой на плоскости. Кривые второго порядка на плоскости, их классификация. Кривая второго порядка может быть задана уравнением
- •Эллипс, его свойства и изображение.
- •Гипербола, её свойства и изображение.
- •Парабола, её свойства и изображение.
- •Системы координат в пространстве.
- •Уравнения плоскости в пространстве. Условия пересечения, параллельности, совпадения и перпендикулярности двух плоскостей в пространстве. Определение угла между двумя плоскостями.
- •Уравнения прямой в пространстве. Условия пересечения, параллельности, совпадения и перпендикулярности двух прямых в пространстве. Определение угла между двумя прямыми.
- •32.Поверхности второго порядка, их классификация и изображения
-
Системы координат в пространстве.
декартовы, цилиндрические и сферические координаты
Декартова система координат в пространстве определяется точкой и базисом из трех векторов. Точка O называется началом координат. Прямые, проведенныечерез начало координат в направлении базисных векторов, называются осями координат. В трехмерном пространстве они называются осями абсцисс, ординат и аппликат. Оси координат являются числовыми осями с началом в точке O , положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора. Координатами точки M называются координаты вектора OM ( радиус–вектора) (см. рис. 1). Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной.
В цилиндрических координатах положение точки M определяется числами ρ , j и z , где ρ и j — полярные координаты точки M' , а z — проекция вектора OM на вектор →n .
В сферических координатах положениеточки M определяется числами ρ , j и θ , где ρ = |OM| , j — полярный угол точки M' , а θ — угол между векторами →n и OM .Мы будем отсчитывать угол θ от вектора →n по направлению к вектору OM . Угол θ принимает значения от 0 до π .
-
Уравнения плоскости в пространстве. Условия пересечения, параллельности, совпадения и перпендикулярности двух плоскостей в пространстве. Определение угла между двумя плоскостями.
Каноническое уравнение плоскости в пространстве:
Аx+By+Cz+D=0, где D = -Ax0-By0-Cz0
Условие
параллельности двух плоскостей
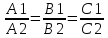
Условие перпендикулярности A1*A2+B1*B2+C1*C2=0
Плоскости
совпадают когда
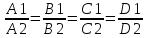
угол между плоскостями находится по формуле:
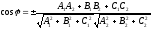
Расстояние
d от точки Мo(Xo;Yo;Zo)
до плоскости Ax+By+Cz+D=0
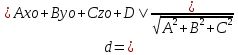
-
Уравнения прямой в пространстве. Условия пересечения, параллельности, совпадения и перпендикулярности двух прямых в пространстве. Определение угла между двумя прямыми.
Параметрические уравнения прямой в пространстве:

Канонические уравнения прямой в пространстве
:![]()
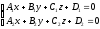
 .
.
32.Поверхности второго порядка, их классификация и изображения
Определение. Поверхности второго порядка – это поверхности, уравнения которых в прямоугольной системе координат являются уравнениями второго порядка.
Цилиндрические поверхности.
Определение. Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой- либо фиксированной прямой.
-
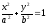 -
эллиптический цилиндр.
-
эллиптический цилиндр. -
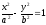 - гиперболический цилиндр.
- гиперболический цилиндр. -
x2 = 2py – параболический цилиндр.
Поверхности вращения.
Определение. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d.
-
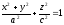 - эллипсоид вращения
- эллипсоид вращения -
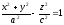 - однополостный
гиперболоид вращения
- однополостный
гиперболоид вращения -
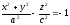 - двуполостный гиперболоид
вращения
- двуполостный гиперболоид
вращения
-
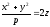 - параболоид вращения
- параболоид вращения -
Сфера:
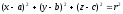
-
Трехосный эллипсоид:
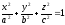
-
Однополостный гиперболоид:
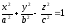
-
Двуполостный гиперболоид:
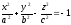
-
Эллиптический параболоид:
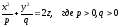
-
Гиперболический параболоид:
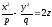
-
Конус второго порядка:
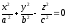
Определение. Цилиндрическими координатами точки М называются числа (r, , h), которые определяют положение точки М в пространстве.
Определение. Сферическими координатами точки М называются числа (r,,), где - угол между и нормалью.
