
- •Производная функции. Дифференцирование суммы, разности, произведения и частного двух функций. Геометрический смысл производной функции.
- •Дифференциал функции, его свойства.
- •Дифференцирование элементарных функций. Табличные производные.
- •Неопределённый интеграл, его свойства.
- •Методы интегрирования: метод непосредственного интегрирования и метод разложения. Табличные интегралы.
- •Метод интегрирования по частям и метод замены переменной под знаком интеграла.
- •Понятие матрицы. Операции над матрицами, их свойства.
- •Квадратная матрица. Треугольная, диагональная, единичная матрицы. Степень квадратной матрицы. Матричный многочлен.
- •Определитель квадратной матрицы. Вычисление определителей второго и третьего порядков.
- •Свойства определителей.
- •Общие способы вычисления определителей.
- •Ранг матрицы, его свойства. Методы нахождения ранга матрицы.
- •Обратная матрица. Теорема о существовании обратной матрицы. Методы нахождения обратной матрицы.
- •Собственные значения матрицы. Собственные и присоединённые векторы матрицы.
- •Комплексные числа, их геометрическая интерпретация.
- •Корень n-ой степени из комплексного числа. Логарифм и степень комплексного числа.
- •Правило Крамера. Решение линейных систем алгебраических уравнений.
- •Системы линейных алгебраических уравнений. Общие понятия. Теорема Кронекера-Капелли.
- •Однородные и неоднородные системы линейных алгебраических уравнений. Теоремы о существовании решений. Структура общего решения.
- •Системы координат на плоскости.
- •Прямая на плоскости. Различные уравнения прямой на плоскости
- •Условия пересечения, параллельности, совпадения и перпендикулярности двух прямых на плоскости. Определение угла между двумя прямыми.
- •Уравнение кривой на плоскости. Кривые второго порядка на плоскости, их классификация. Кривая второго порядка может быть задана уравнением
- •Эллипс, его свойства и изображение.
- •Гипербола, её свойства и изображение.
- •Парабола, её свойства и изображение.
- •Системы координат в пространстве.
- •Уравнения плоскости в пространстве. Условия пересечения, параллельности, совпадения и перпендикулярности двух плоскостей в пространстве. Определение угла между двумя плоскостями.
- •Уравнения прямой в пространстве. Условия пересечения, параллельности, совпадения и перпендикулярности двух прямых в пространстве. Определение угла между двумя прямыми.
- •32.Поверхности второго порядка, их классификация и изображения
-
Неопределённый интеграл, его свойства.
Определение:
Неопределенным интегралом функции
f(x) называется
совокупность первообразных функций,
которые определены соотношением.

1*
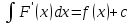
2* (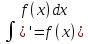
3*
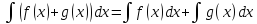
4*

5*

6*
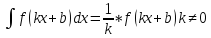
7*
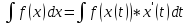 формула замены переменных
формула замены переменных
8*
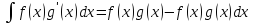 формула интегрирования по частям
формула интегрирования по частям
-
Методы интегрирования: метод непосредственного интегрирования и метод разложения. Табличные интегралы.
-
Метод не посредственного интегрирования
Базовый метод свойства 1* и 6* и табличные интегралы
А.
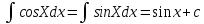
Б.
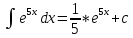
F(x)=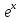
F(5x)=
В.
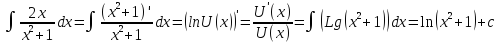
-
Метод разложения.
База метода свойства 3*,4*,5*,6* и табличные интегралы.
А.
 =
=
=2|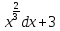 |
|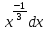 =
=
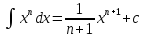
Табличные интегралы
-

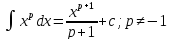
-
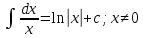
-
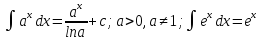 dx=
dx=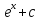
-
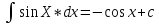
-
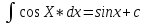
-
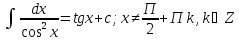
-
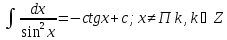
-
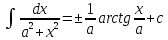 ;
a
;
a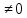
-
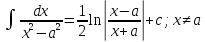
-
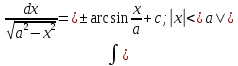
-
 C
C
-
Метод интегрирования по частям и метод замены переменной под знаком интеграла.
7*
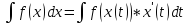 формула замены переменных
формула замены переменных
8*
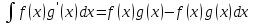 формула интегрирования по частям
формула интегрирования по частям
-
Метод замены переменных
Теорема: Если требуется
найти интеграл
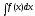 ,
но сложно отыскать первообразную, то с
помощью замены x = (t)
и dx = (t)dt
получается:
,
но сложно отыскать первообразную, то с
помощью замены x = (t)
и dx = (t)dt
получается:

Пример. Найти неопределенный
интеграл
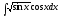 .
.
Сделаем замену t = sinx, dt = cosxdt.
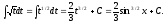
Пример.
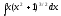
Замена
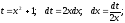 Получаем:
Получаем:
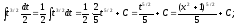
-
Интегрирование по частям.
Способ основан на известной формуле производной произведения: (uv) = uv + vu
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем:
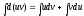 ,
а в соответствии с приведенными выше
свойствами неопределенного интеграла:
,
а в соответствии с приведенными выше
свойствами неопределенного интеграла:
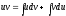 или
или
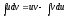 ;
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример.

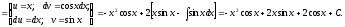
Пример.
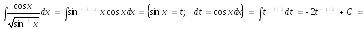
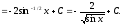
Пример.
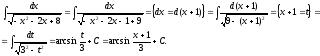
-
Понятие матрицы. Операции над матрицами, их свойства.
Матрица размером MxN называется совокупностью M и N чисел, расположенных в виде прямоугольных таблиц из M строк и N столбцов
Элементом матрицы (i и j) называется число расположенное на пересечении итой строки и джитого столбца матрицы
Операции над матрицами
А.Сложение матриц
Это сумма матриц А и В одинакового размера MxN, называется квадратные матрицы MxN, которые определяются по формуле Сij=Aij+Bij
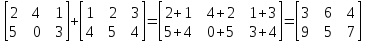
Б. умножение матриц
Произведение матрицы А размера М и Х называется матрица В размерами М и Х, такая что Вij=P*aij, где Р это любое число.
5* =
=
В. Вычитание матриц
Разность А-В матриц элементами ij одинакового размера M и X называется матрица С размерами М и Х такая что Cij=Aij-Bij
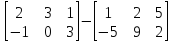 =
=
Г. Произведение матриц
Необходимое условие: количество столбцов матрица А равно количеству строк матрицы В.
Произведение матрицы А размерами М х К на матрицу В размерами К и N называется матрица С размерами М и К. такая что Cij=Ai1*B1j+Ai2*B2j+Ai3*B3j…+Aik*Bkj
Примеры
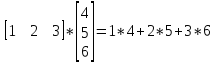
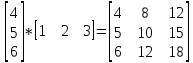
A*B=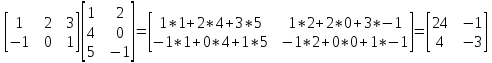
B*A=
Свойства
1.) Сложение и вычитание допускается только для матриц одинакового размера.
2.) Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть A + Θ = A
3.) Все элементы нулевой матрицы равны нулю.
4.) Возводить в степень можно только квадратные матрицы.
5.) Ассоциативность сложения: A + (B + C) = (A + B) + C.
6.) Коммутативность сложения: A + B = B + A.
7.) Ассоциативность умножения: A(BC) = (AB)C.
8.) Дистрибутивность умножения относительно сложения:
A(B + C) = AB + AC;
(B + C)A = BA + CA.
9.) Свойства операции транспонирования матриц:
(AT)T = A
(AB)T = BTAT
(A − 1)T = (AT) − 1, если обратная матрица A - 1 существует.
(A + B)T = AT + BT
detA = detAT
10.) Умножение матриц не коммутативно, т.е. АВ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными
11.) Если произведение АВ определено, то для любого числа верно соотношение:
(AB) = (A)B = A(B).
