70. Опишите портфель из двух бумаг в случае полной корреляции.

Дисперсия портфеля из двух бумаг равна:

В случае полной корреляции .

Для квадрата риска дисперсии портфеля получаем:

==

Если извлечь корень из обеих частей получится

Так как все переменные не отрицательны, то модуль можно опустить. Получаем:

Заменяя так что получим

Это уравнение отрезка (АВ), где точки А и В имеют следующие координаты:

t пробегает значения от 0 до 1. При t=0 портфель находится в точке А, при t=1 – в точке В. Таким образом, допустимое множество портфелей в случае полной корреляции ценных бумаг представляет собой отрезок (АB)

71. Опишите портфель из двух бумаг в случае полной антикорреляции.

→

→

Возможен портфель нулевого риска:

→

Т.к. 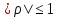все допустимые портфели цен бум лежат внутри треугольника АВС

- доходность портфеля нулевого риск при антикорреляции

- портфель нулевого риска в случае полной антикорреляции

72. Найдите портфель минимального риска из двух независимых бумаг и его доходность.

Найти портфель минимального риска

Функция Лагранжа

→ → →

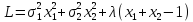
- портфель минимального риска при 2 незав бум

- доходность портфеля

73. Для портфеля из трех независимых бумаг найдите портфель минимального риска и его доходность.

Найти портфель минимального риска

Функция Лагранжа

,

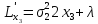
Выразим через

Отсюда:

– портфель минимального риска в случае трех независимых бумаг

– доходность портфеля

76. Выведите уравнение минимальной границы .

-

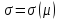Для нахождения искомого уравнения необходимо подставить

в выражение для :

Следовательно, подставляя в данное выражение условие получаем:

откуда

A

M

B

77. Доказать, что уравнение минимальной границы является ветвью гиперболы и найти ее асимптоты.

к каноническому виду

Полный квадрат в правой части уравнения:

Каноническое уравнение минимальной границы имеет вид:

=1 или

где

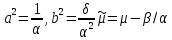
Минимальная граница представляет собой ветвь гиперболы с асимптотами

и абсолютным минимумом

Уравнение асимптот:

78. Найдите портфель Марковица минимального риска при заданной ожидаемой доходности .

Наряду с задачей (1) , при условиях и найдём портфель минимального риска из всех портфелей эффективности не менее заданной – задача (1’). Такой портфель назовём портфелем Марковица.

Для нахождения портфеля рассмотрим оптимизационную задачу: найти минимум целевой функции

при условиях и .

=>

79. Опишите портфель Тобина.

Найти портфель минимального риска из всех портфелей заданной эффективности.

при

Переформулируем задачу, исключив .

Составим функцию Лагранжа.

Выразим X из первого, подставим во второе.

Обозначим:

80. Докажите, что прямая является касательной к графику минимальной границы .

Для доказательства найдём точки пересечения гиперболы и прямой 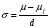, решая совместно их уравнения, убедимся, что такая точка одна.

Приравнивая правые части и , получим

=.

Далее получим квадратное относительно µ уравнение и найдём его корни:

.

Дискриминант данного уравнения равен нулю:

.

Это доказывает, что прямая является касательной к графику минимальной границы .

Найдём теперь координаты точки касания (координаты касательного портфеля):

Итак, эффективность касательного портфеля µ_T равна:

.

Подставляя найденное значение эффективности µ_T в уравнение касательной, найдём риск касательного портфеля σ_Т:

Итак, для координат касательного портфеля имеем