10.2.2. Геометрия прямозубых цилиндрических колес.
Профили зубьев
зубчатых колес выполнены по эвольвенте.
Эвольвента (кривая BC
на рис. 10.4) - это кривая, описываемая
точкой отрезка, перекатываемого без
скольжения по окружности; эту окружность
называют основной. Эвольвентный
профиль обеспечивает постоянство
передаточного отношения передачи,
высокую прочность и долговечность
зубьев колес, относительно малое
скольжение на рабочих поверхностях
зубьев и, следовательно, высокий КПД.
Благодаря этим свойствам колеса с
зубьями эвольвентного профиля получили
широкое применение в машиностроении.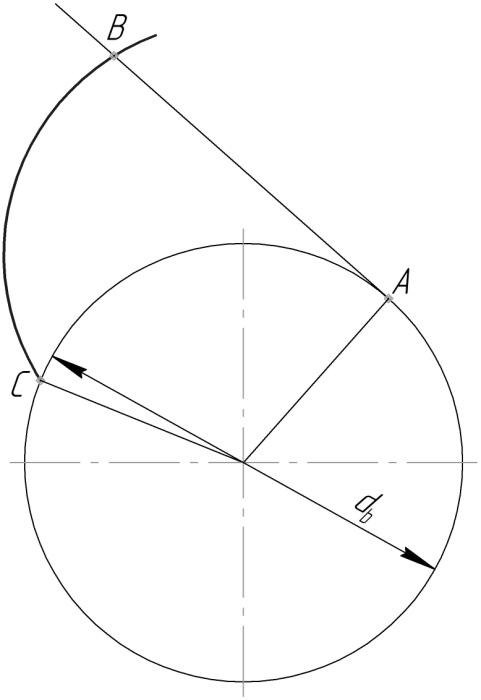
Геометрия и основные параметры зубчатого зацепления цилиндрических прямозубых колес (нарезанных без смещения режущего инструмента) показаны на рис. 10.5:
Рис. 10.4.
и
- диаметры окружностей выступов зубьев;
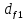и
- диаметры окружностей впадин зубьев;
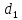и
- диаметры делительных окружностей
шестерни и колеса (на делительном
диаметре толщина зуба равна ширине
впадины, а их сумма - окружному делительному
шагу);
и
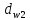- диаметры начальных окружностей шестерни
и колеса (начальные окружности
перекатываются одна по другой без
скольжения). Для зубчатых колес, нарезанных
без смещения,
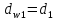и
;
и
- диаметры основных окружностей шестерни
и колеса;
- высота зуба, где
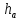- высота головки зуба;
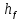- высота ножки зуба (причем, обычно
,
);
-
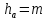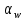угол зацепления стандартизован и равен
(угол между линией зацепления и прямой,
перпендикулярной межосевой линии);
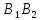- активная линия
зацепления (траектория общей точки
контакта сопряженных зубьев при ее
движении);
Рис. 10.6.
- угол наклона
зубьев (угол между плоскостью, проходящей
через ось зубчатого колеса и боковой
поверхностью зуба), см. рис. 10.6, б и в.
Угол наклона:
- для косых зубьев
;
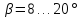- для шевронных
зубьев
.
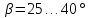- окружной шаг
зубьев (расстояние между одноименными
профилями (точками) соседних зубьев по
дуге концентрической окружности
(делительной, начальной и т.д.) зубчатого
колеса), см. рис. 10.6, а, б, в;
- нормальный шаг
зубьев (косых, шевронных и арочных);
кратчайшее расстояние (по нормали
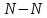к профилю зуба) по одной из соосных
поверхностей (делительной, начальной
и т.д.) зубчатого колеса, см. рис. 10.6, б и
в:
.
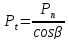У
прямозубых колес
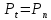(рис. 10.6, а).
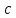- радиальный зазор
между головкой и впадиной зубьев
сопряженного колеса;
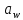- межосевое
расстояние, мм:
.
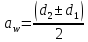Знак минус подставляют для внутреннего зацепления.
При работе передачи в зацеплении находится одновременно одна или несколько пар зубьев. Количественной оценкой многопарности зацепления является коэффициент торцевого перекрытия:
,
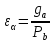где
- длина активной линии зацепления (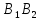
).
Например, если коэффициент торцевого
перекрытия
,
то это значит, что
времени работы передачи в зацеплении
находится одна пара зубьев, а
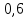времени работы передачи - две пары
зубьев.
На практике для
расчета
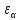пользуются приближенной формулой:
.
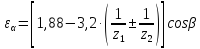В
прямозубых передачах коэффициент
торцевого перекрытия
(обычно
),
в косозубых, шевронных и с круговым
зубом -
.
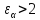С увеличением коэффициента перекрытия
повышается плавность зацепления зубьев,
уменьшаются динамические нагрузки на
них и снижается шум, возникающий при
работе передачи. Поэтому в быстроходных
и высоконагруженных передачах вместо
прямых зубьев применяют косые, шевронные
и арочные зубья.
Для прямозубых
колес длина окружности делительного
диаметра
связана с числом зубьев
и шагом
:
⇒
,
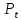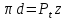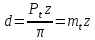где
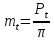- окружной модуль зубьев. Тогда для
косых, шевронных и арочных зубьев модуль
определяется также в нормальном
направлении и называется нормальным
модулем:
.
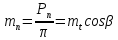Для
прямых зубьев
.
Так как делительная
окружность является базовой при
определении размеров зубьев, то размеры
зубьев цилиндрических зубчатых колес
вычисляют по делительному нормальному
модулю, который называют модулем
зацепления
.
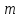Модуль зацепления
- основная характеристика размеров
зубчатых и червячных колес. Модули
стандартизованы в диапазоне
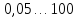мм (ГОСТ 9563-60).