45. Решение матричных игр: аффинные преобразования.
Определение. Преобразование плоскости называется аффинным, если
-
оно взаимно однозначно;
-
образом любой прямой является прямая.
Преобразование называется взаимно однозначным, если
-
разные точки переходят в разные;
-
в каждую точку переходит какая-то точка.
Однородные координаты
Определение. Однородные координаты — координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же число.
Однородными координатами вектора (х, у) является тройка чисел (x', y', h), где х = х' / h, у = y'/h, а h — некоторое вещественное число (случай, когда h = 0 является особым).
Прим. Данные координаты не позволяют однозначно задать точку плоскости. Например, (1, 1, 1) и (2, 2, 2) задают одну и ту же точку (1, 1). Предлагается взять набор (x, y, 1), который будет описывать все точки плоскости.
Матрица преобразования для однородных координат имеет размер 3х3. Рассмотрим некоторые преобразования в однородных координатах.
Сжатие/растяжение
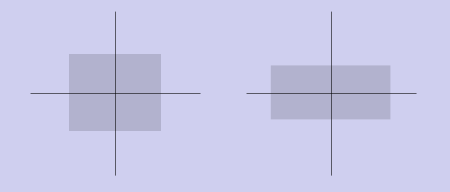
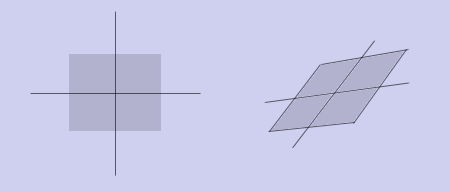
Это преобразование умножает соответствующие координаты точек на коэффициенты масштабирования по осям: (x, y) -> (ax * x, ay * y). Матрица преобразования запишется следующим образом:
[ ax 0 0 ]
[ 0 ay 0 ]
[ 0 0 1 ]
Где ax – растяжение по оси x,
ay – растяжение по оси y.
Прим. Можно заметить, что при отрицательных значениях коэффициентов сжатия/растяжения происходит отражение относительно соответствующих осей. Этот случай можно включить в данное преобразование, а можно вынести в отдельное, сказав, что коэффициенты масштабирования принимают только положительные значения.
Поворот
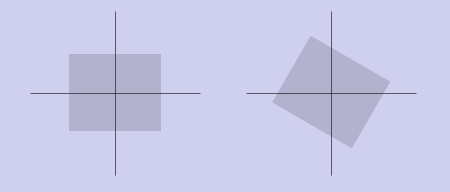
Матрица поворота 2x2 была подробно разобрана ранее. Теперь она дополняется строкой и столбцом:
[ cos(phi) sin(phi) 0 ]
[ -sin(phi) cos(phi) 0 ]
[ 0 0 1 ]
Прим. При угле phi = п эта матрица задает центральную симметрию относительно начала координат, которая является частным случаем поворота. Можно заметить, что такую симметрию можно задать с помощью преобразования сжатия/растяжения (допуская отрицательные коэффициенты масштабирования).
Параллельный перенос
Исходный вектор (x, y) переходит в (x + tx, y + ty). Матрица преобразования запишется следующим образом:
[ 1 0 0 ]
[ 0 1 0 ]
[ tx ty 1 ]
Отражение
Как говорилось в примечании к преобразованию сжатия/растяжения, отражения получаются следующим образом:
[ -1 0 0 ]
[ 0 1 0 ]
[ 0 0 1 ] отражение относительно оси x
[ 1 0 0 ]
[ 0 -1 0 ]
[ 0 0 1 ] отражение относительно оси y
Общий вид аффинного преобразования
Матрица 3x3, последний столбец которой равен ( 0 0 1 )T, задает аффинное преобразование плоскости:
[ * * 0 ]
[ * * 0 ]
[ * * 1 ]
По одному из свойств, аффинное преобразование можно записать в виде:
f(x) = x * R + t,
где R – обратимая матрица 2x2, а t – произвольный вектор. В однородных координатах это запишется следующим образом:
[ R1,1 R1,2 0 ]
[ R2,1 R2,2 0 ]
[ tx ty 1 ]
Если умножить вектор-строку на эту матрицу получаем результат преобразования:
[ x y 1 ] * [ R1,1 R1,2 0 ]
[ R2,1 R2,2 0 ]
[ tx ty 1 ]
=
[ x’ y’ 1 ] + [ tx ty 1 ]
При этом [ x’ y’ ] = R * [ x y ]
Прим. При аффинном преобразовании площади всех фигур изменяются в |R|. Т.о. аффинное преобразование представляется в виде композиции некоторого преобразования, задаваемого матрицей R, и параллельного переноса.
Матрица R определяет новый базис плоскости. Т.е. вектор (1, 0) переходит в (R1,1, R1,2), вектор (0, 1) переходит в (R2,1, R2,2). Новый базис это строки матрицы R.
Пример.
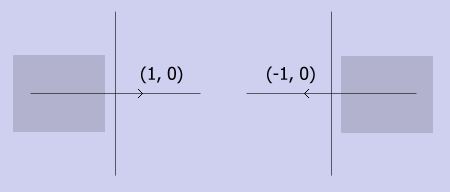При
отражении относительно оси y, базисный
вектор по оси ординат сохраняется, а по
оси абсцисс переходит в (-1, 0). Т.о. матрица
R будет выглядеть следующим образом:
[ -1 0 ] [ 0 1 ] Теперь становится ясно, что кроме вышеперечисленных преобразований, с помощью аффинного преобразования можно получить скос:
