Решить задачу

Z = Зх₁ + х₂à max

при ограничениях:

4x_l + Зх₂ < 18,

x₁ + 2x₂ £ 6,

0 £ x₁ £ 5,

0 £ x₂ £ 4,

х₁, x₂ - целые числа.

Решение. За нижнюю границу линейной функции примем, например, ее значение в точке (0,0), т.е. Z₀ = Z (0; 0) = 0.

I этап. Решая задачу симплексным методом, получим Z_max = 13 при Х₁^*= = (4,5; 0; 0; 1,5; 0,5; 4); так как первая компонента х₁^* дробная, то из области решения исключается полоса, содержащая дробное оптимальное значение х₁^*, т.е. 4 < х₁ < 5. Поэтому задача 1 разбивается на две задачи 2 и 3:

Задача 2 Задача 3

Z=3x₁+x₂→max Z=3x₁+x₂→max

при ограничениях: при ограничениях:

4x_l + Зх₂ < 18 4x₁+3x₂<18

x₁ + 2x₂ £ 6 x₁ + 2x₂ £ 6

0 £ x₁ £ 4 5 £ x₁ £ 5

0 £ x₂ £ 4 0 £ x₂ £ 4

х₁, x₂ - целые числа. х₁, x₂ - целые числа.

Список задач: 2 и 3. Нижняя граница линейной функции не изменилась: Z₀=0.

II этап. Решаем (по выбору) одну из задач списка, например задачу 3 симплексным методом.

Получим, что условия задачи 3 противоречивы.

III этап. Решаем задачу 2 симплексным методом. Получим Z_max =14/3 при X₃^*= (4; 2/3; 0; 2/3; 0; 10/3). Хотя Z(X₃^*) = 14/3 > Z₀ = 0, по-прежнему сохраняется Z₀ = 0, ибо план нецелочисленный. Так как х₂^* - дробное число, из области решений исключаем полосу 0 < x₂ < 1 и задачу 2 разбиваем на две задачи 4 и 5.

Задача 4 Задача 5

Z=3x₁+x₂→max Z=3x₁+x₂→max

при ограничениях: при ограничениях:

4x_l + Зх₂ < 18 4x_l + Зх₂ < 18

x₁ + 2x₂ £ 6 x₁ + 2x₂ £ 6

0 £ x₁ £ 4 0 £ x₁ £ 4

0 £ x₂ £ 0 1 £ x₂ £ 4

х₁, x₂ - целые числа. х₁, x₂ - целые числа.

Список задач: 4 и 5. Значение Z₀ = 0.

IV этап. Решаем задачу 4 симплексным методом.

Получим Z_max = 12 при X₄^* = (4; 0; 2; 2; 0; 0). Задачу исключаем из списка, но при этом меняем Z₀; Z₀ = Z(X₄^*) = 12, ибо план Х₄^* целочисленный.

V этап. Решаем задачу 5 симплексным методом.

Получим Z_max = 12,25 при X₅^* = (3,75; 1; 0; 0,25; 0,25; 0; 3). Z ₀ не меняется, т.е. Z₀ = 12, ибо план X₅^* нецелочисленный. Так как х₁^* - дробное, из области решений исключаем полосу 3<x₁<4, и задача 5 разбивается на две задачи: 6 и 7.

Задача 6 Задача 7

Z=3x₁+x₂→max Z=3x₁+x₂→max

при ограничениях: при ограничениях:

4x_l + Зх₂ < 18 4x_l + Зх₂ < 18

x₁ + 2x₂ £ 6 x₁ + 2x₂ £ 6

0 £ x₁ £ 3 4 £ x₁ £ 4

1 £ x₂ £ 4 1 £ x₂ £ 4

х₁, x₂ - целые числа. х₁, x₂ - целые числа.

Список задач: 6 и 7. Значение Z₀ = 12.

VI этап. Решаем одну из задач списка, например задачу 7, симплексным методом.

Получим, что условия задачи 7 противоречивы (рис. 3).

VII этап. Решаем задачу 6 симплексным методом.

Получим Z_max = 10,5,при X₆^* = (3; 1,5; 1,5; 0; 0; 0,5; 2,5). Так как Z(X₆^*) = =10,5 < Z₀ = 12, то задача исключается из списка.

Итак, список задач исчерпан и оптимальным целочисленным решением исходной задачи будет X^* = Х₄^* = (4; 0; 2; 2; 0; 0), а оптимум линейной функции Z_max = 12.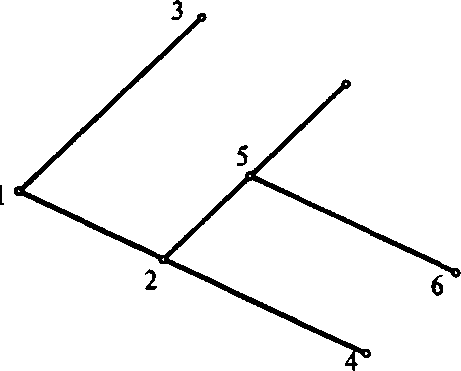

Рис. 3

1 Квадратичное программирование

Под квадратичным программированием понимаются задачи следующего вида (в матричных обозначениях)

где -симметричная матрица размерности . Задачи линейного программирования являются частным случаем этих задач - они получаются при =0.

Способы решения этих задач во многом определяются видом матрицы : если - положительно определённая матрица, то целевая функция будет выпуклой и любой её локальный минимум будет глобальным. Если - отрицательно определённая матрица, то может быть несколько локальных минимумов, но глобальный минимум, если он существует, достигается обязательно на вершине допустимой области. В общем случае, когда собственные числа матрицы имеют разные знаки, задача очень сильно усложняется, так как глобальный минимум может достигаться где угодно - и внутри области и на её границе.

Выпуклое программирование

Под задачей выпуклого программирования понимают задачу вида

где и - выпуклые функции. Для этих задач характерно то, что любой локальный минимум оказывается глобальным, и все сводится к нахождению этого единственного минимума.

Для решения задач этого типа разработаны многочисленные численные методы, приспособленные для решения на ЭВМ, в основном связанные с понятием градиента целевой функции и основной идеей о том, что функция наиболее быстро убывает, если двигаться в направлении, противоположном градиенту. К ним относятся метод градиентного спуска, метод сопряженных градиентов и т.д. Но есть и методы, основанные на других идеях ¾ метод штрафных функций, многочисленные варианты метода случайного поиска и т.д.

Геометрическое программирование

Под задачами геометрического программирования понимают задачи наиболее плотного расположения некоторых объектов в заданной двумерной или трехмерной области. Такие задачи встречаются в задачах раскроя материала для производства каких-то изделий и т.п. Это - еще недостаточно разработанная область математического программирования и имеющиеся здесь алгоритмы в основном ориентированы на сокращение перебора вариантов с поиском локальных минимумов.

Дробно линейное програмирование

Отдельными классами задач математического программирования являются задачи целочисленного, параметрического и дробно-лилейного программирования.

В задачах дробно-линейного программирования целевая функция представляет собой отношение двух линейных функций, а функции, определяющие область возможных изменений переменных, также являются линейными.

2. . Економічна постановка і математична модель задачі нелінійного програмування

Досить детально розглянута в розділах, присвячених лінійному програмуванню, задача пошуку оптимальних обсягів виробництва ґрунтується на припущеннях про лінійність зв’язку між витратами ресурсів і обсягами виготовленої продукції; між ціною, рекламою та попитом тощо. Якщо такі зв’язки насправді є нелінійними, то більш адекватні математичні моделі доцільно формулювати в термінах нелінійного програмування.

Нехай для деякої виробничої системи необхідно визначити план випуску продукції, за умови найкращого способу використання ресурсів системи. Відомі загальні запаси кожного ресурсу, нормативи витрат кожного ресурсу на одиницю продукції та ціна реалізації одиниці виготовленої продукції. Критерії оптимальності можуть бути різноманітними, наприклад максимізація виручки від реалізації продукції. Така умова подається лінійною залежністю загальної виручки від обсягів проданого товару та ціни одиниці продукції.

Однак, загально відомим є факт, що за умов ринкової конкуренції питання реалізації продукції є досить складним. Обсяг збуту кінцевої продукції визначається перш за все її ціною, отже в якості цільової функції доцільно розглядати максимізацію не всієї виготовленої, а лише реалізованої продукції. Тоді необхідно визначити також і оптимальне значення ціни одиниці продукції при якій обсяг збуту буде максимальним, для цього її потрібно ввести в задачу як невідому величину, при цьому обмеження задачі мають враховувати зв’язки між ціною, рекламою та обсягами збуту продукції. Цільова функція міститиме добуток двох невідомих величин (оптимальна ціна одиниці продукції та оптимальна кількість відповідного виду продукції) отже є нелінійною. Таким чином маємо задачу нелінійного програмування.

І нарешті будь-яка задача стає нелінійною, якщо в математичній моделі необхідно враховувати умови невизначеності та ризик. В якості величини ризику розповсюджене використання такої величини як дисперсія, тому врахування обмеженості ризику вимагає введення нелінійної функції в систему обмежень, а мінімізація ризику певного процесу досягається за рахунок дослідження математичної моделі з нелінійною цільовою функцією.

Загальна задача математичного програмування формулюється наступним чином:

Знайти такі значення змінних x_j , щоб цільова функція набувала екстремального (максимального чи мінімального значення): (5.33)

за умов ()(5.34)

(5.35)

Якщо всі функції та () є лінійними, то приходимо до задачі лінійного програмування, інакше (хоча б одна з функцій не є лінійною) маємо задачу нелінійного програмування.