29)Определение границ устойчивости двойственных оценок.

1 Нахождение интервалов устойчивости двойственной оценки по отношению к изменениям ресурсов каждого типа

обратная матрицы В составленная из компонентов векторов ,, базиса, который определяет оптимальный план задачи взятых из столбцов векторов ,, образующий первоначальный единичный базис

=*=

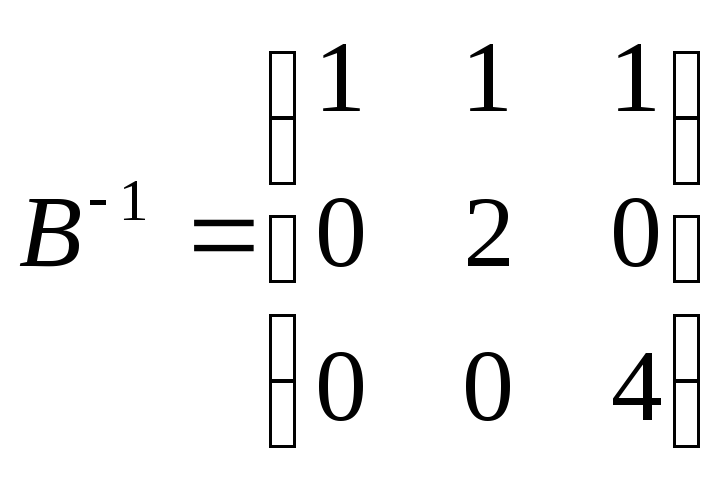
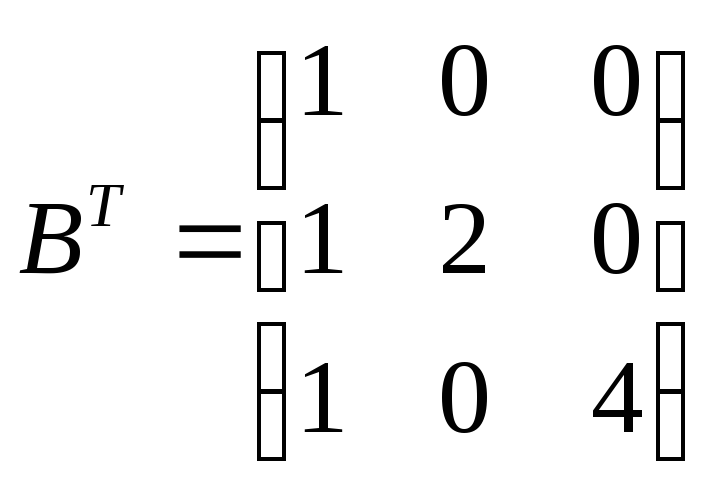
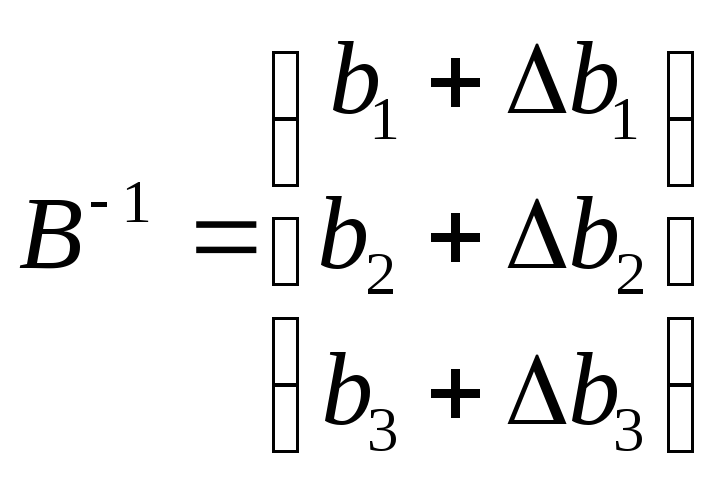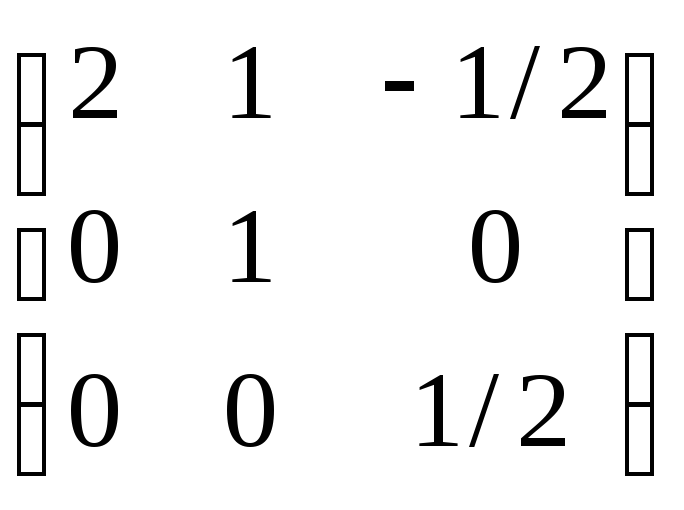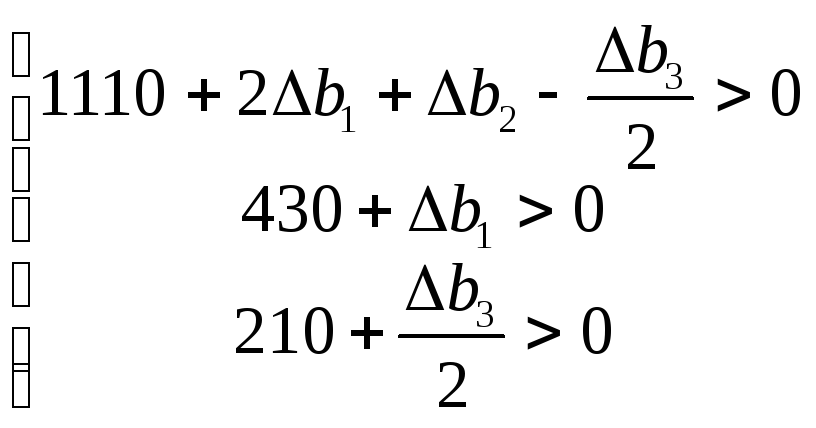
если

Очевидно если это означает, что если количество ресурсов I типа будет увеличено в пределах 555,то несмотря на это оптимальным планом двойственной задачи остаётся план Y(0;5/2:1/2).

Далее если

если

если III тип ресурса принадлежит соответственно , а количество остальных ресурсов остается первоначальным, то двойственная задача имеет один и тот же план.

Если найдено решение задачи, то нетрудно провести анализ устойчивости двойственных оценок относительно изменений . Это, в свою очередь, позволяет:

1. проанализировать устойчивость оптимального плана задачи , относительно изменений свободных членов системы линейных уравнений

2. оценить степень влияния изменения , на максимальное значение целевой функции задачи , что дает возможность определить наиболее целесообразный вариант возможных изменений .

30) Экономические примеры, математическая постановка задачи целочисленного программирования.

Целочисленное программирование — разновидность математического программирования, подразумевающая, что искомые значения должны быть целыми числами.

Раздел математического программирования, в котором изучаются методы нахождения экстремумов функций в пространстве параметров, где все или некоторые переменные являются целыми числами.

Простейший метод решения задачи целочисленного программирования — сведение её к задаче линейного программирования с проверкой результата на целочисленность.

В математической модели задачи целочисленного программирования как целевая функция, так и функции в системе ограничений могут быть линейными, нелинейными и смешанными.

Постановка задачи целочисленного программирования

По смыслу значительной части экономических задач, относятся к задачам линейного программирования, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. К ним относятся, например, задачи, в которых переменные означают количество единиц неделимой продукции, число станков при загрузке оборудования, число судов при распределениях по линиям, число турбин в энергосистеме, число вычислительных машин в управляющем комплексе и многие другие.

Задача линейного целочисленного программирования формируется следующим образом: найти такое решение (план) X = (x₁,x₂,...,x_n), при котором линейная функция

(1)

принимает максимальное или минимальное значение при ограничениях

=b_i, i=1, 2…, m. (2)

х_j ³ 0, j=1, 2,..., п. (3)

x_j - целые числа (4)

К настоящему времени разработано значительное количество частных методов решения конкретных типов задач целочисленного программирования. Тем не менее, почти все эти методы и их модификации можно описать на основе единой принципиальной схемы, состоящей из трех элементов.

Элемент 1. Предусматривается процедура формирования и решения последовательности взаимосвязанных задач, которые называют задачами, порожденными исходной задачей, или задачами-истоками. При этом оптимальное решение по крайней мере одной из задач-истоков должно совпадать с оптимальным решением породившей их задачи.

Элемент 2. Каждой задаче, порожденной исходной задачей, ставится в соответствие так называемая ослабленная задача (задача с ослабленными ограничениями), оптимальное решение которой может быть найдено с гораздо меньшими затратами, чем оптимальное решение соответствующей ей задачи-истока. Специфика ослабленной задачи чаще всего заключается в том, что ее система ограничений является менее жесткой по сравнению с системой ограничений задачи-истока и определяет множество допустимых решений, содержащее все допустимые решения задачи-истока. Как правило, в целочисленном программировании ослабленная задача представляет собой задачу линейного программирования с ограничениями, более слабыми, чем в соответствующей целочисленной задаче-истоке. Очевидно, что если ослабленная задача не имеет допустимых решений, то их не имеет и задача-исток. В некоторых модификациях методов целочисленного программирования целевая функция ослабленной задачи также может отличаться от целевой функции задачи-истока. В этом случае оптимальное значение целевой функции ослабленной задачи (т.е. значение, соответствующее оптимальному решению) должно быть не меньше оптимального значения целевой функции задачи-истока, если речь идет о задаче максимизации. Кроме того, оптимальное значение целевой функции ослабленной задачи определяет (для задачи максимизации) верхнюю границу для оптимального значения целевой функции задачи-истока.

Элемент 3. В результате анализа решения ослабленной задачи в зависимости от специфики метода, как правило, принимается решение, относящееся к задаче-истоку:

а) исключить ее из рассмотрения;

б) заменить одной порожденной задачей, выбранной по специальному правилу из определенной совокупности;

в) заменить системой порожденных задач.

Следует отметить, что существуют и другие подходы к решению задач целочисленного программирования, которые в общем случае не гарантируют нахождения оптимального решения, но приводят к допустимому решению, близкому (в смысле значения целевой функции) к оптимальному, а иногда и совпадающему с ним. В основе одного из таких подходов лежит идея использования случайной выборки допустимых решений с последующим улучшением (в смысле значения целевой функции) каждого из них, когда возможность улучшения допустимого решения достаточно просто обнаружить.

Проиллюстрируем метод ветвей и границ на примере.