15. Симплекс-метод с искусственным базисом.

Метод искусственного базиса применяется, когда задача не имеет начального опорного решения, т.е. отсутствуют базисные переменные в системе ограничений.

Согласно данному методу для решаемой задачи составляется расширенная задача, которую решают симплекс-методом и на основе полученного решения либо находят для исходной задачи оптимальное решение, либо устанавливается причина его отсутствия.

Чтобы составить расширенную задачу в исходную задачу вводят искусственные переменные. Искусственными переменными называют неотрицательные переменные, которые вводят в ограничение неравенства для получения начального опорного решения с базисом. Каждая искусственная переменная вводится в левую часть с коэффициентом _1 и в целевую функцию в задаче на максимум с коэффициентом –М и коэффициентом +М в задаче на минимум, где число М сколь угодно большое по сравнению с 1.

В общем случае расширенная задача на максимум имеет вид:

Z(x)=C₁x₁+C₂x₂+…+C_nx_n-Mx_n+1-Mx_n+2-…-Mx_n-m → max

Ограничение:

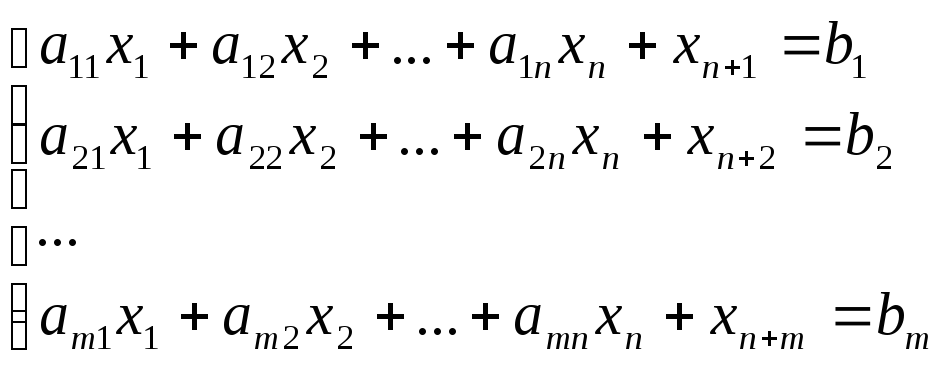
x_j≥0; j=

Теорема 1.

Любому допустимому решению исходной задачи Х^/=(x₁^/, x₂^/, …, x_n^/) соответствует допустимое решение расширенной задачи X^/=(x₁^/, x₂^/, …, x_n^/, 0, 0, …, 0).

Теорема 2.

Значение целевой функции расширенной задачи на максимум (минимум) на любом допустимом решении X^/=(x₁^/, x₂^/, …, x_n^/, 0, 0, …, 0), у которого все искусственные переменные равны 0 больше (меньше) значения целевой функции на любом допустимом решении, у которого хотя бы одна искусственная переменная отлична от 0.

Теорема 3.

Если расширенная задача имеет оптимальное решение X^*=(x₁^*, x₂^*, …, x_n^*, 0, 0, …, 0), у которого все искусственные переменные равны 0, то исходная задача будет иметь оптимальное решение X^*=(x₁^*, x₂^*, …, x_n^*).

Теорема 4.

Если расширенная задача имеет оптимальное решение, в котором хотя бы 1 искусственная переменная отлична от 0, то исходная задача не имеет решения в виду несовместности системы ограничений.

Теорема 5.

Если расширенная задача не имеет решения в виду неограниченности целевой функции, то исходная задача также не имеет решения по той же причине.

Особенности метода:

1)В виду того, что начальное опорное решение расширенной задачи содержит переменные, входящие в целевую функцию в задаче на максимум с коэффициентом –М, в задаче на минимум с коэффициентом –М оценки разложений k состоят из двух слагаемых, одно из которых не зависит от М, а другое – зависит. Так как М сколь угодно велико по сравнению с 1, то на первом этапе расчёта последнюю оценочную строку делят на две части.

2)Векторы, соответствующие искусственным переменным, которые выводятся из базиса, в дальнейшем исключаются из рассмотрения.

3)После того, как все искусственные переменные исключатся из базиса, расчёты продолжаются обычным симплекс-методом.

16. Симметричные двойственные задачи и правила их построения.

Любой задаче линейного программирования можно поставить в соответствие другую задачу, которую называют двойственной или сопряжённой.

Например, составить двойственную задачу к задаче использования ресурсов.

Имеется m видов сырья в количестве b₁, b₂, …, b_m, которые используют для изготовления n видов продукции. Известно, что на единицу каждого вида продукции расходуется a_ij количество сырья, где i=, j=. Пусть C_j – прибыль при реализации j-того вида продукции.

Математическая модель данной задачи имеет вид:

Z(x)=C₁x₁+C₂x₂+…+C_nx_n → max

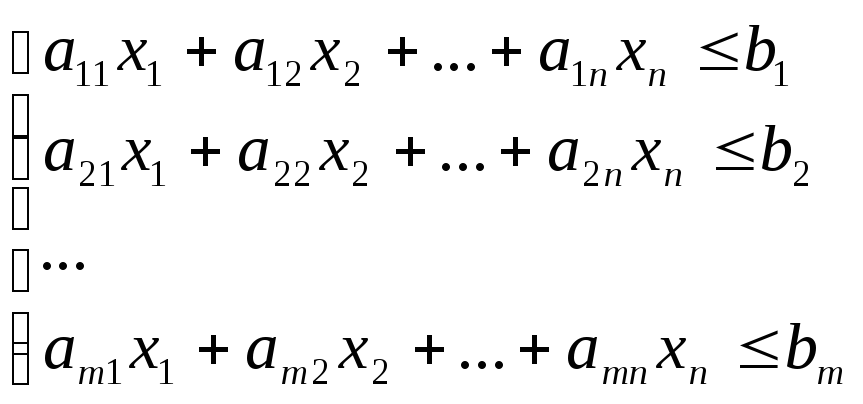
x_j≥0; j=

Предположим, что второй производитель хочет перекупить сырьё.

Составим двойственную задачу, решение которой позволит определить условие продажи сырья. Введём цены видов сырья: I=y₁, II=y₂, …, N=y_m. Затраты на приобретение i-того вида сырья в количестве b_i=b_iy_i. Второму производителю выгодно минимизировать суммарные затраты на приобретение всех видов сырья. По этому целевая функция задачи имеет вид: F(y)=b₁y₁+b₂y₂+…+b_my_m → min

Первому производителю не выгодно продать сырьё, если суммарная стоимость всех видов сырья, расходуемых на каждое изделие j-той продукции a_1jy₁+a_2jy₂+…+a_mjy_m≤C_j.

Тогда система ограничений задачи имеет вид.

y_j≥0; j=

Связь исходной и двойственной задач состоит в том, что коэффициенты C_j исходной задачи являются свободными членами системы ограничений двойственной задачи. А свободные члены системы ограничений исходной задачи служат коэффициентами целевой функции двойственной задачи. Матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи.

Двойственные задачи бывают симметричными и несимметричными.

Симметричные пары:

1)если Z(x) → max, Ах≤А₀, х≥0, то F(y) =YA₀→ min, YA≥С, y≥0;

2)если Z(x) → min, Ах≥А₀, х≥0, то F(y) =YA₀→ max, y≥0.

Общие правила составления двойственных задач:

1)Во всех ограничения исходной задачи свободные члены должны находится в правой части, а члены с независимыми – в левой.

2)Ограничения неравенства исходной задачи должны быть записаны так, чтобы знаки неравенств у них были направлены в одну сторону.

3)Если знаки неравенств в исходной задаче ≤, то целевая функция должна стремится к максимуму, если знаки ≥, то должна стремится к минимуму.

4)Целевая функция двойственной задачи F(y)=с₀+b1y1+b₂y₂+…+b_my_n → min, где с₀ – свободный член целевой функции Z(x).

5)Целевая функция F(y) должна оптимизироваться противоположным, по сравнению с Z(x), образом.

6)Каждому неизвестному x_j исходной задачи соответствует ограничение в двойственной задаче.