5. Принципы построения экономико-математичеких моделей

1. Принцип достаточности исходной информации. В каждой модели должна использоваться только та информация, которая известна с точностью, требуемой для получения реультатов моделирования.

2. Принцип инвариантности (однозначности) информации требует, чтобы входная информация, используемая в модели, была независима от тех параметров моделируемой системы, которые еще неизвестны на данной стадии исследования.

3. Принцип преемственности. Сводится к тому, что каждая последующая модель не должна нарушать свойств объекта, установленных или отраженных в предыдущих моделях.

4. Принцип эффективной реализуемости. Необходимо, чтобы модель могла быть реализована при помощи современных вычислительных средств.

6, Экономико-математические модели включают в себя систему ограничений, целевую функцию.

Система ограничений состоит из отдельных математических уравнений или неравенств, называемых балансовыми уравнениями или неравенствами.

Целевая функция связывает между собой различные величины модели. Как правило, в качестве цели выбирается экономический показатель (прибыль, рентабельность, себестоимость, валовая продукция и т.д.). Поэтому целевую функцию иногда называют экономической, критериальной. Целевая функция - функция многих переменных величин и может иметь свободный член.

Критерии оптимальности - экономический показатель, выражающийся при помощи целевой функции через другие экономические показатели. Одному и тому же критерию оптимальности могут соответствовать несколько разных, но эквивалентных целевых функций. Модели с одной и той же системой ограничений могут иметь различные критерии оптимальности и различные целевые функции.

Решением экономико-математической модели, или допустимым планом называется набор значений неизвестных, который удовлетворяет ее системе ограничений. Модель имеет множество решений, или множество допустимых планов, и среди них нужно найти единственное, удовлетворяющее системе ограничений и целевой функции. Допустимый план, удовлетворяющий целевой функции, называется оптимальным. Среди допустимых планов, удовлетворяющих целевой функции, как правило, имеется единственный план, для которого целевая функция и критерий оптимальности имеют максимальное или минимальное значение. Если модель задачи имеет множество оптимальных планов, то для каждого из них значение целевой функции одинаково.

Если экономико-математическая модель задачи линейна, то оптимальный план достигается в крайней точке области изменения переменных величин системы ограничений. В случае нелинейной модели оптимальных планов и оптимальных значений целевой функции может быть несколько. Поэтому необходимо определять экстремальные планы и экстремальные значения целевой функции. План, для которого целевая функция модели имеет экстремальное значение, называют экстремальным планом, или экстремальным решением.

Для нелинейных моделей иногда существуют экстремальные значения целевой функции, а для линейных моделей экстремальных планов и экстремальных значений целевой функции быть не может.

Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение.

Методика построения экономико-математической модели состоит в том, чтобы экономическую сущность задачи представить математически, используя различные символы, переменные и постоянные величины, индексы и другие обозначения.

Все условия задачи необходимо записать в виде уравнений или неравенств. Поэтому, в первую очередь необходимо определить систему переменных величин, которые могут для конкретной задачи обозначить искомый объем производства продукции на предприятии, количество перевозимого груза поставщиками конкретным потребителям.

7, Общая и типовая задача в линейном программировании.

Оптимизационная задача - это экономико-математическая задача, которая состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.

В самом общем виде задача математически записывается так:

U = f(X) max; X W,

Где X = (Х1, Х2,…, Хn);

W - область допустимых значений переменных Х1, Х2,…, Хn;

f(X) - целевая функция.

Для того, чтобы решить задачу оптимизации, достаточно найти ее оптимальное решение, т.е. указать X() W такое, что f(X()) f(X), при любом X W, или для случая минимизации - что f(X()) ? f(X), при любом X W.

Оптимизационная задача является неразрешимой, если она не имеет оптимального решения. В частности, задача максимизации будет неразрешима, если целевая функция f(X) не ограничена сверху на допустимом множестве W.

Методы решения оптимизационных задач зависят как от вида целевой функции f(X), так и от строения допустимого множества W. Если целевая функция в задаче является функцией n переменных, то методы решения называют методами математического программирования.

В математическом программировании принято выделять следующие основные задачи в зависимости от вида целевой функции f(X) и от области W:

· задачи линейного программирования, если f(X) и W линейны;

· задачи целочисленного программирования, если ставится условие целочисленности переменных Х1, Х2,…, Хn;

· задачи нелинейного программирования, если форма f(X) носит нелинейный характер.

Задачи линейного программирования.

Задачей линейного программирования называется задача исследования операций, математическая модель которой имеет вид:

f(X) = СjXj max(min);

aij xj = bi, iI, IM = 1, 2,…m;

aij xj bi, iM;

Xj0, jJ, JN = 1, 2,…n.

При этом система линейных уравнений и неравенств, определяющая допустимое множество решений задачи W, называется системой ограничений задачи линейного программирования, а линейная функция f(X) называется целевой функцией или критерием оптимальности.

Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалентна минимизации той же функции, взятой с противоположным знаком, и наоборот.

Правило приведения задачи линейного программирования к каноническому виду состоит в следующем:

1) если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции;

2) если в ограничениях правая часть отрицательна, то следует умножить это ограничение на -1;

3) если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобразуются в равенства;

4) если некоторая переменная Хk не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными::

Xk = X`k - Xl, где l - свободный индекс, X`k 0, Xk 0.

8, 1. Каждому опорному/базисному решению ЗЛП соответствует крайняя угловая точка выпуклого многогранника D, представляющего собой область допустимых решений задачи (*),и наоборот.

2. Целевая функция z ЗЛП (*) достигает своего оптимума в крайней точке выпуклого многогранника D, порожденного условиями задачи (*). Если целевая функция z ЗЛП (*) достигает своего оптимума более чем в одной крайней точке выпуклого многогранника D, порожденного условиями задачи (*), то она достигает своего оптимума в любой точке, являющейся выпуклой комбинацией данных крайних точек.

Линейное программирование — раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.      Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Отсюда — необходимость разработки новых методов.

Теорема. Если система векторов  содержит m линейно независимых векторов , то допустимый план                                        (2. 10)      является крайней точкой многогранника планов.      Теорема. Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией.

9, Для более полного представления о задаче линейного программирования сделаем её геометрическую интерпретацию. Совокупность любого числа линейных ограничений выделяет в пространстве x1, x1,..., xn некоторый выпуклый многогранник, ограничивающий область допустимых значений переменных (ОДЗП). Геометрическую интерпретацию и решение задачи линейного программированиянетрудно получить лишь в простейших случаях при n = 2 или n = 3. Рассмотрим задачу: max{F(x)= c1x1+ c2x2|( aj1x1+ aj2x2)≥(≤)bj,j=1,m; x1≥0, x2≥0}.

Каждое из ограничивающих неравенств определяет полуплоскость, лежащую по одну сторону прямой a aj1x1+ aj2x2)=bj , j = 1,m. ОДЗП получится в результате пересечения m полуплоскостей. Условия неотрицательности позволяют ограничиться рассмотрением положительного квадранта.

На рис. 1 показан один из возможных вариантов ОДЗП в виде замкнутого многоугольника для случая m = 3.

Рисунок 1 - Графическая интерпретация задачи линейного программирования

Координаты x1 и x2 любой точки, принадлежащей области, удовлетворяют системе ограничений задачи линейного программирования. Чтобы найти оптимальное решение, зададим функции цели некоторое постоянное значение F1 = c1x1 + c2x2 = const и построим прямую F1, которая будет отсекать на оси ординат (x1 = 0) отрезок , x2=F1/c2 а на оси абсцисс (x2=0) – отрезок x1=F1/c1. Если задать другие значения функции цели F2 , F3 ,... и изобразить соответствующие линии, то получим семейство параллельных прямых, которые называются линиями уровня функции цели. Направление стрелки показывает направление увеличения целевой функции F1 < F2 < F3 < .... Величину функции цели можно характеризовать расстоянием d от начала координат до линии уровня в соответствии с выражением d=(F1/F2)cosα.

В теории линейного программирования доказано, что если оптимальное решение задачи линейного программирования существует и единственно, то оно достигается в некоторой вершине многоугольника решений. Очевидно, что целевая функция достигает максимального значения тогда, когда её линия будет проходить через точку M. Координаты этой точки будут оптимальным решением задачи. Минимальное значение рассматриваемой функции будет достигаться в начале координат. Таким образом, если требуется определить такие x1 и x2, которые обеспечивают максимум функции цели, то геометрически это означает, что необходимо провести прямую F = const , проходящую хотя бы через одну вершину области и имеющую максимальное расстояние d от начала координат.

В случае минимизации это расстояние должно быть минимальным. В зависимости от вида ОДЗП и расположения линий уровня могут встретиться случаи, изображенные на рис. 2.

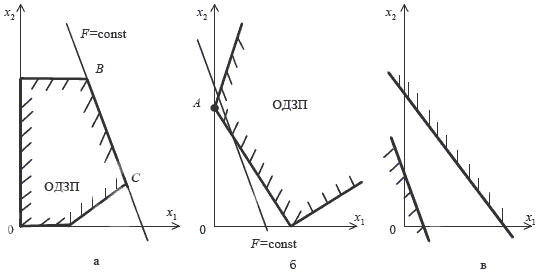
Рис. 2 - Различные варианты решения задач линейного программирования

На рис.2, а функция F достигает минимума в начале координат. При максимизации функции ее линия совпадает со стороной ВС, ограничивающей ОДЗП. Координаты любой точки отрезка ВС будут доставлять максимум функции F, что соответствует бесчисленному множеству оптимальных решений задачи линейного программирования.

На рис. 2, б ОДЗП не замкнута, целевая функция сверху не ограничена, т.е. максимального значения не имеет. Минимальное значение функция принимает в точке A.

На рис. 2, в приведен случай несовместных ограничений, в этом случае функция цели не имеет ни максимума, ни минимума, так как ОДЗП представляет собой пустое множество.

10.Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно.

Пусть задача линейного программирования задана в двумерном пространстве, то есть ограничения содержат две переменные. Найти минимальное значение функции

При

(2) : a11x1+a22x2<= b1, a21x1+a22x2<=b2

X1,x2>0

Допустим, что система (2) при условии (3) совместна и её многоугольник решений ограничен. Каждое из неравенств (2) и (3), как отмечалось выше, определяет полуплоскость с граничными прямыми: . Линейная функция (1) при фиксированных значениях  является уравнением прямой линии: . Построим многоугольник решений системы ограничений (2) и график линейной функции (1) при . Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая  опорная и функция  при этом достигает минимума.

Значения  возрастают в направлении вектора , поэтому прямую  передвигаем параллельно самой себе в направлении вектора . Прямая дважды становится опорной по отношению к многоугольнику решений (в точках  и ), причем минимальное значение принимает в точке . Координаты точки  находим, решая систему уравнений прямых  и .

Если многоугольник решений представляет собой неограниченную многоугольную область, то возможны два случая.

Случай 1. Прямая , передвигаясь в направлении вектора  или противоположно ему, постоянно пересекает многоугольник решений и ни в какой точке не является опорной к нему. В этом случае линейная функция не ограничена на многоугольнике решений как сверху, так и снизу.

Случай 2. Прямая, передвигаясь, всё же становится опорной относительно многоугольника решений. Тогда в зависимости от вида области линейная функция может быть ограниченной сверху и неограниченной снизу, ограниченной снизу и неограниченной сверху, либо ограниченной как снизу, так и сверху.