
- •1. Парная регрессия
- •1.1. Спецификация модели
- •1.2. Парная линейная регрессия. Оценка параметров. Экономическая интерпретация
- •1.3. Основные предположения регрессионного анализа
- •1.4. Статистические свойства оценок. Проверка статистической значимости в парной линейной регрессии
- •1.5. Доверительные интервалы для оценок параметров. Доверительные интервалы прогноза для парной линейной регрессии
- •1.6. Метод Гольдфельда—Квандта проверки гипотезы гомоскедастичности
- •2. Множественная регрессия
- •2.1. Спецификация модели
- •2.2. Множественная линейная регрессия. Оценка параметров. Экономическая интерпретация
- •3. Системы одновременных уравнений
- •4. Временные ряды
- •4.1. Компоненты временных рядов
- •4.2. Критерии случайности
- •4.3. Оценка тренда и периодической составляющей
- •4.4. Критерий Дарбина—Уотсона
- •4.5. Сглаживание временного ряда с помощью простой скользящей средней
- •4.6. Сглаживание временного ряда с помощью взвешенной скользящей средней
- •4.7. Сглаживание временного ряда с помощью скользящей медианы
- •5. Практические задания
- •5.1. Лабораторная работа № 1. Парная линейная регрессия
- •5.2. Лабораторная работа № 2. Метод Гольдфельда—Квандта проверки гипотезы гомоскедастичности
- •5.3. Лабораторная работа № 3. Множественная линейная регрессия
- •5.4. Лабораторная работа № 4. Макроэкономическая модель Кейнса
- •5.5. Лабораторная работа № 5. Проверка случайности ряда наблюдений
- •5.6. Лабораторная работа № 6. Оценка тренда и периодической составляющей
- •5.7. Лабораторная работа № 7. Сглаживание временного ряда с помощью простой скользящей средней
- •5.8. Лабораторная работа № 8. Критерий Дарбина—Уотсона
- •5.9. Лабораторная работа № 9. Подбор и оценка тренда с помощью встроенных средств Excel
- •5.10. Тест по парной и множественной регрессии
- •6. Рекомендуемая литература
- •8. Приложения. Статистические таблицы
- •8.1. Приложение 1. Стандартное нормальное распределение
- •8.2. Приложение 2. Критические значения -критерия Стьюдента
- •8.3. Приложение 3. Критические значения -критерия Фишера
- •8.4. Приложение 4. Критические значения статистики Дарбина—Уотсона
- •8.5. Приложение 5. Критические значения распределения
- •199034, С.-Петербург, Университетская наб., 7/9
- •199061, С.-Петербург, Средний пр., 41.
2.2. Множественная линейная регрессия. Оценка параметров. Экономическая интерпретация
В случае нескольких
объясняющих переменных часто используют
линейную модель, в которой функциональная
зависимость имеет вид
![]() .
Для нахождения оценок неизвестных
параметров
.
Для нахождения оценок неизвестных
параметров
![]() используют метод наименьших квадратов.
Этот метод дает хорошие результаты,
если выполнены основные предположения
о случайной составляющей, объединенные
в первую группу основных предположений
регрессионного анализа. Согласно этому
методу значения параметров эмпирической
зависимости
используют метод наименьших квадратов.
Этот метод дает хорошие результаты,
если выполнены основные предположения
о случайной составляющей, объединенные
в первую группу основных предположений
регрессионного анализа. Согласно этому
методу значения параметров эмпирической
зависимости
![]() выбираются таким образом, чтобы
минимизировать сумму квадратов отклонений
фактических значений показателя от
расчетных:
выбираются таким образом, чтобы
минимизировать сумму квадратов отклонений
фактических значений показателя от
расчетных:
![]() .
.
Применяя тот же прием, что и в случае парной регрессии (вычисляем производные по неизвестным параметрам и приравниваем их к нулю) приходим к системе так называемых нормальных уравнений метода наименьших квадратов. В матричном виде система записывается следующим образом:

где
 ,
,
 ,
,
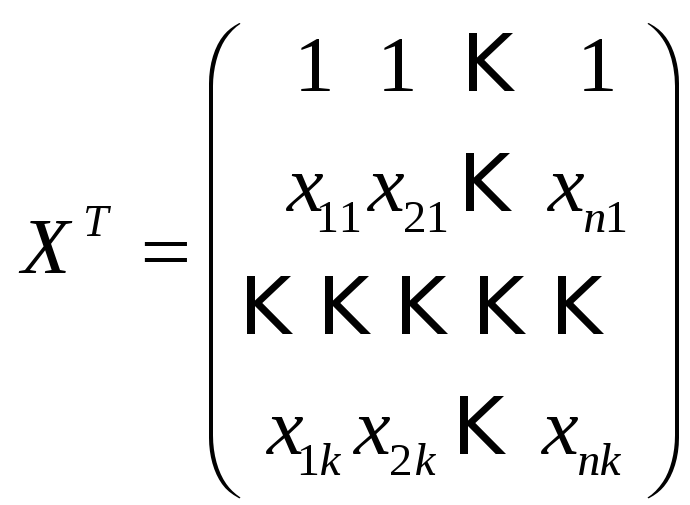 .
.
Если матрица
![]() невырождена, то решение системы уравнений
дается выражением:
невырождена, то решение системы уравнений
дается выражением:
 .
.
Найденное решение
называется оценкой наименьших квадратов
неизвестных параметров
![]()
Таким образом, множественная линейная регрессия имеет вид
![]() .
.
Значения показателя,
рассчитанные по линейной регрессии для
тех значений объясняющих факторов,
которые содержались в выборке обозначим
через
![]() :
:
![]() .
.
Нетрудно найти остатки (разности между фактическими значениями показателя и значениями, вычисленными по уравнению линейной регрессии):
![]() .
.
При выполнении предположений из первой группы основных предположений регрессионного анализа доказана теорема Гаусса—Маркова о том, что найденные оценки неизвестных параметров обладают свойством несмещенности и являются наилучшими линейными оценками.
Оценка средней относительной ошибки аппроксимации так же, как и в случае парной линейной регрессии, производится по формуле:
![]() .
.
Аналогично случаю парной линейной регрессии можно показать, что статистика

является
несмещенной оценкой дисперсии
![]() .
.
В случае множественной регрессии важную роль играют частные коэффициенты корреляции. Дело в том, что коэффициенты парной корреляции могут давать ложное представление о силе взаимосвязи между двумя переменными, так как они не учитывают влияние других переменных. Явление ложной корреляции хорошо известно в статистической литературе. Для оценки «истинной» взаимозависимости используются коэффициенты частной корреляции «очищенные» от влияния других факторов. Ограничимся определением коэффициентов частной корреляции только для случая двух переменных.
Частные
коэффициенты корреляции
![]() и
и
![]() в случае двух переменных (
в случае двух переменных (![]() )
вычисляются по формулам
)
вычисляются по формулам
![]() ,
,
![]() ,
,
где
![]() — коэффициенты парной корреляции.
— коэффициенты парной корреляции.
Коэффициент детерминации определяется так же, как и в случае парной регрессии:
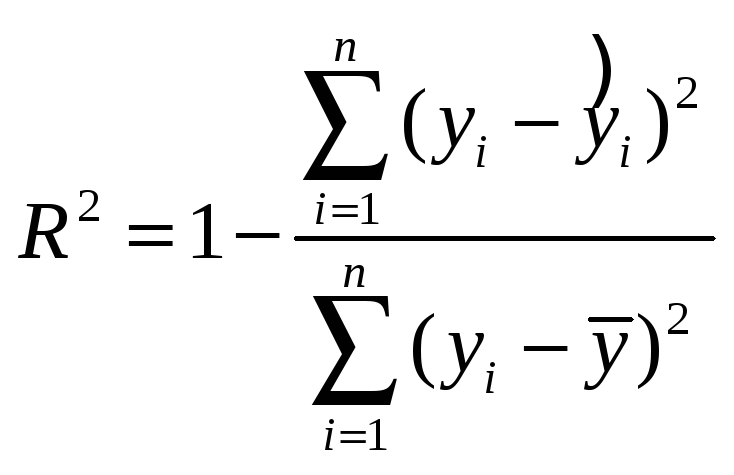 .
.
Статистическая
значимость множественной регрессии в
целом оценивается с помощью
![]() -критерия
Фишера:
-критерия
Фишера:
Если выполнены
предположения регрессионного анализа,
то при выполнении гипотезы
![]() (что означает отсутствие взаимосвязи
между
(что означает отсутствие взаимосвязи
между
![]() и
и
![]() ,
а также статистическую незначимость
построенной парной регрессии) статистика
,
а также статистическую незначимость
построенной парной регрессии) статистика
![]() распределена по закону Фишера с числом
степеней свободы числителя равным
распределена по закону Фишера с числом
степеней свободы числителя равным
![]() и числом степеней свободы знаменателя
равным
и числом степеней свободы знаменателя
равным
![]() (т.е.
(т.е.
![]() ).
).
На основе этого факта построен критерий проверки значимости линейной регрессии в целом.
Правило проверки
значимости линейной регрессии в целом
(гипотезы
![]() )
с использованием
)
с использованием
![]() -статистики:
-статистики:
Вычислить значение
![]() -статистики:
-статистики:
-
если
 ,
то гипотезу
,
то гипотезу
 следует отклонить и, следовательно,
признать построенное уравнение линейной
регрессии статистически значимым;
следует отклонить и, следовательно,
признать построенное уравнение линейной
регрессии статистически значимым; -
если
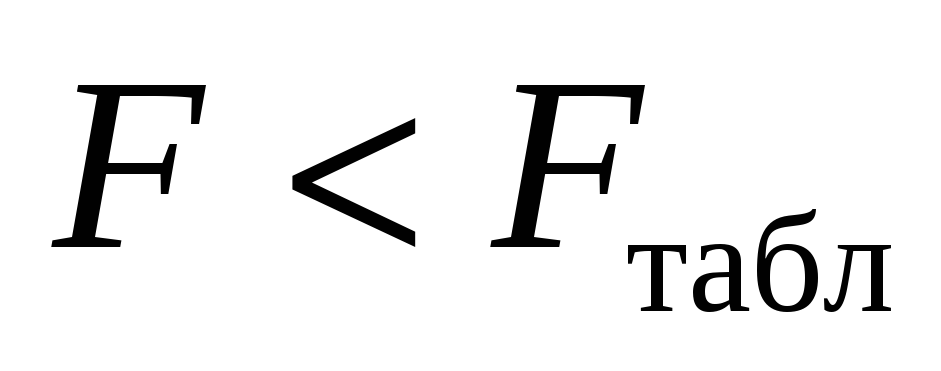 ,
то гипотезу
,
то гипотезу
 следует принять и, следовательно,
признать построенное уравнение
статистически не значимым.
следует принять и, следовательно,
признать построенное уравнение
статистически не значимым.
Значение
![]() определяется по таблице распределения
Фишера при степенях свободы
определяется по таблице распределения
Фишера при степенях свободы
![]() и уровне значимости 5%.
и уровне значимости 5%.
Кроме того, при выполнении предположений регрессионного анализа справедливы следующие утверждения:
-
статистика
 распределена по закону Стьюдента с
распределена по закону Стьюдента с
 степенями свободы (т.е.
степенями свободы (т.е.
 ),
здесь
),
здесь
 ,
где
,
где
 — первый элемент, стоящий на главной
диагонали матрицы
— первый элемент, стоящий на главной
диагонали матрицы
 ;
; -
статистика
 распределена по закону Стьюдента с
распределена по закону Стьюдента с
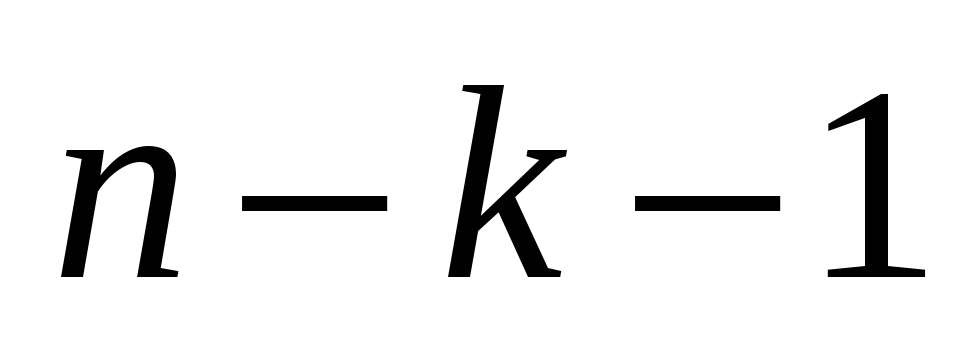 степенями свободы, (т.е.
степенями свободы, (т.е. ),
здесь
),
здесь
 ,
где
,
где
 —
—
 -й
элемент, стоящий на главной диагонали
матрицы
-й
элемент, стоящий на главной диагонали
матрицы
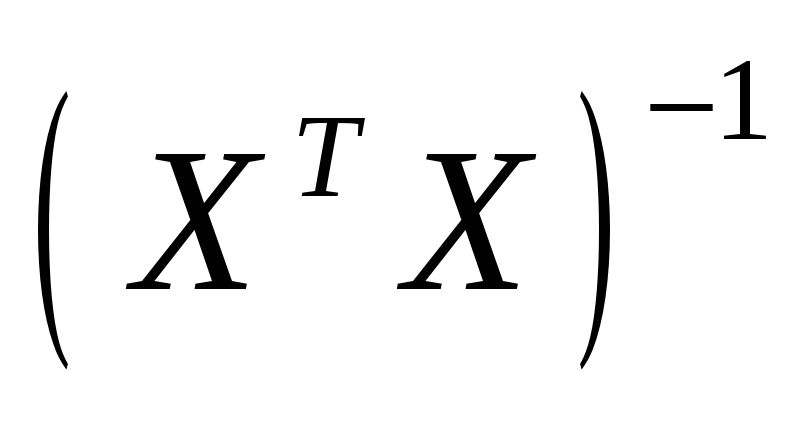 .
.
Правило проверки
статистической значимости оценок
![]() и
и
![]() ,
основывается на проверке статистических
гипотез
,
основывается на проверке статистических
гипотез
![]() и
и
![]() .
Невозможность отклонения какой-либо
из гипотез означает статистическую
незначимость соответствующего
коэффициента и, наоборот, отклонение
какой-либо из гипотез означает, что
соответствующий коэффициент статистически
значим.
.
Невозможность отклонения какой-либо
из гипотез означает статистическую
незначимость соответствующего
коэффициента и, наоборот, отклонение
какой-либо из гипотез означает, что
соответствующий коэффициент статистически
значим.
Правило проверки
значимости коэффициента
![]()
Вычислить статистику
![]() .
Статистика
.
Статистика
![]() при выполнении гипотезы
при выполнении гипотезы
![]() распределена по закону Стьюдента с
распределена по закону Стьюдента с
![]() степенями свободы, поэтому:
степенями свободы, поэтому:
-
если
 ,
то гипотезу
,
то гипотезу
 следует отклонить и, следовательно,
признать коэффициент
следует отклонить и, следовательно,
признать коэффициент
 статистически
значимым;
статистически
значимым; -
если
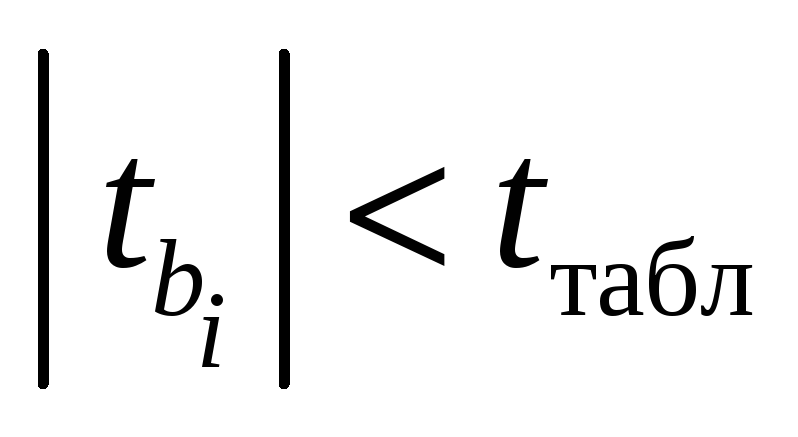 ,
то гипотезу
,
то гипотезу
 следует принять и, следовательно,
признать коэффициент
следует принять и, следовательно,
признать коэффициент
 статистически незначимым.
статистически незначимым.
Значение
![]() определяется из таблицы распределения
Стьюдента при
определяется из таблицы распределения
Стьюдента при
![]() степенях свободы как критическая точка,
соответствующая двусторонней критической
области с уровнем значимости 5%.
степенях свободы как критическая точка,
соответствующая двусторонней критической
области с уровнем значимости 5%.
Правило проверки
значимости коэффициента
![]()
Вычислить статистику
![]() .
Статистика
.
Статистика
![]() при выполнении гипотезы
при выполнении гипотезы
![]() распределена по закону Стьюдента с
распределена по закону Стьюдента с
![]() степенями свободы, поэтому:
степенями свободы, поэтому:
-
если
 ,
то гипотезу
,
то гипотезу
 следует отклонить и, следовательно,
признать коэффициент
следует отклонить и, следовательно,
признать коэффициент
 статистически значимым;
статистически значимым; -
если
 ,
то гипотезу
,
то гипотезу
 следует принять и, следовательно,
признать коэффициент
следует принять и, следовательно,
признать коэффициент
 статистически незначимым.
статистически незначимым.
Значение
![]() определяется из таблицы распределения
Стьюдента при
определяется из таблицы распределения
Стьюдента при
![]() степенях свободы как критическая точка,
соответствующая двусторонней критической
области с уровнем значимости 5%.
степенях свободы как критическая точка,
соответствующая двусторонней критической
области с уровнем значимости 5%.
Экономическая
интерпретация коэффициентов при
объясняющих факторах та же, что и в
случае парной регрессии. Коэффициент
![]() показывает, на сколько единиц изменится
значение показателя, если значение
фактора
показывает, на сколько единиц изменится
значение показателя, если значение
фактора
![]() ,
соответствующего этому коэффициенту,
увеличится на одну единицу, в то время
как остальные факторы останутся
неизменными.
,
соответствующего этому коэффициенту,
увеличится на одну единицу, в то время
как остальные факторы останутся
неизменными.
