5.4. Лабораторная работа № 4. Макроэкономическая модель Кейнса

Простейшая макроэкономическая модель Кейнса экономики страны имеет следующий вид:

(1)

где — личное потребление в постоянных ценах; — национальный доход в постоянных ценах; — инвестиции в основной капитал и в запасы экспорта и импорта; — случайная составляющая, ; — параметры (неизвестные) линейной зависимости потребления от . В этой модели и — эндогенные переменные, — экзогенная переменная. Система уравнений (1) задает структурную форму модели.

Для построения оценок и параметров используется косвенный метод наименьших квадратов (КМНК). Для его применения строится система приведенных уравнений, в которой эндогенные переменные и выражаются через экзогенную переменную :

(2)

Здесь — параметры, определяемые через структурные коэффициенты и ; случайная составляющая u определяется через случайную составляющую и структурный коэффициент .

Далее по известным данным , строятся оценки коэффициентов парных линейных регрессий

(3)

после чего из второго уравнения выражается через и подставляется в первое уравнение. В результате получаем эмпирическое выражение функции

, (4)

где и — оценки структурных параметров и соответственно.

Практическое задание

1. Постройте приведенную форму (2) модели Кейнса. Для этого получите аналитически выражение коэффициентов через коэффициенты и структурной формы модели (1), а также выражение случайной составляющей через .

2. Смоделируйте выборку из 20 наблюдений . Для этого:

1. задайте произвольно 20 значений экзогенной переменной ;

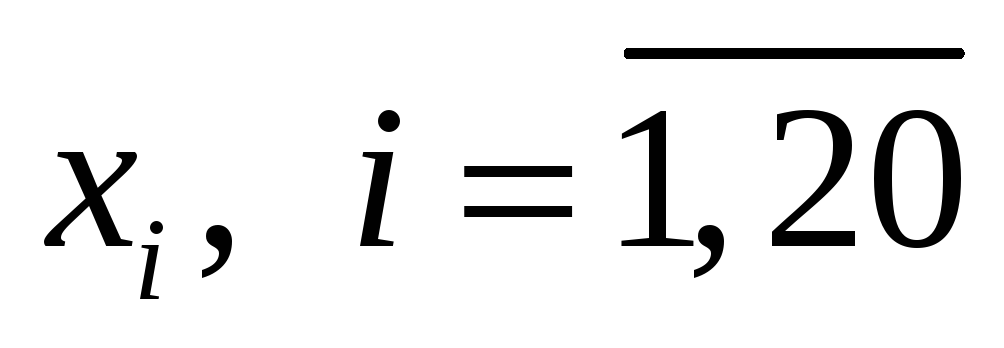2. значения случайной составляющей , возьмите из нормального распределения ; при построении значений можно воспользоваться функциями СЛЧИС и НОРМОБР или возможностями пакета Анализ данных;

3. значения и задайте произвольно;

4. по полученным ранее значениям 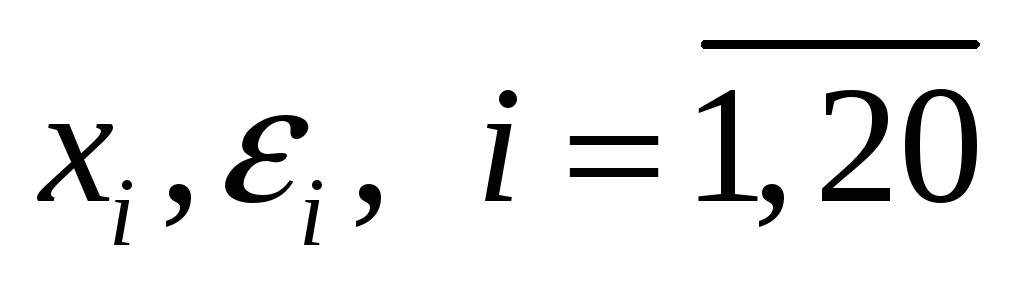, с помощью системы приведенных уравнений (2) и выражения коэффициентов через коэффициенты и найдите соответствующие значения .

3. По полученным в п. 2 данным найдите оценки коэффициентов двух парных линейных регрессий (3). Для нахождения оценок воспользуйтесь функцией ЛИНЕЙН.

4. Используя полученные в п. 3 оценки коэффициентов парных регрессий (3), найдите зависимость (4) значений от , т.е. получите аналитическое выражение коэффициентов и , которые, в свою очередь, являются, оценками структурных коэффициентов и .

5. Для того чтобы убедиться в преимуществе подобного метода построения оценок структурных коэффициентов, сравним полученные оценки с оценками, определяемыми при построении «прямых» регрессий. Для этого, воспользовавшись значениями , вычисленными в п. 2, постройте парную регрессию на методом наименьших квадратов с помощью функции ЛИНЕЙН:

.

6. Сравните оценку , найденную в п. 4, и оценку , полученную в п. 5.

7. Выполните все предыдущие вычисления для . Сравните результаты.

8.Оформите отчет, в котором:

1. приведите исходные данные, найденные значения и ;

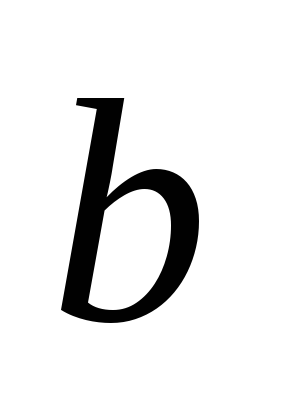2. на одной диаграмме постройте график зависимости из (1) и график зависимости из (4); сравните с графиком зависимости 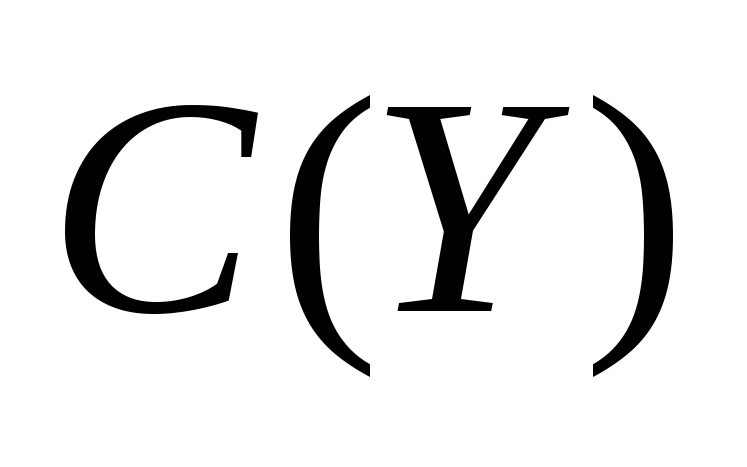из п. 5;

3. проверьте значимость полученных парных линейных регрессий в п.3 с помощью коэффициента детерминации и -статистики (воспользуйтесь стандартной функцией ЛИНЕЙН);

4. для уравнения (4), полученного в п. 4, также проверьте статистическую значимость, вычислив и -статистику по соответствующим формулам;

5. сравните коэффициенты и значимость парных регрессий (п. 4, 5), сравните также для этих уравнений значения средних ошибок аппроксимации; сделайте выводы о преимуществах различных методов.