1. Реальный газ. Уравнение Ван-дер-Ваал ьса

Полученное в предыдущей лекции уравнение состояния идеального газа не является универсальным. Оно оказывается справедливым при достаточно малых давлениях (и плотностях) и выполняется тем точнее, чем меньше давление. По мере же увеличения давления газа его свойства все более отклоняются от свойств идеального газа и, в конце концов, наступает его конденсация в жидкость.

В этом нет ничего удивительного, если вспомнить те допущения, которые были сделаны при выводе уравнения состояния идеального газа. В самом деле, идеальный газ мы определили как газ, состоящий из молекул, не

взаимодействующих между собой, а сами молекулы при этом считали материальными точками, т.е. мы пренебрегали их размерами и объемом. Однако оба эти допущения являются приближенными.

Так, например, если при атмосферном давлении среднее расстояние между молекулами в 10 раз превосходит их собственные размеры, то при давлении в 100 атм молекулы газа в среднем удалены друг от друга на расстояние, которое только вдвое больше их размеров. В этих условиях объемом молекул нельзя пренебречь, а силы взаимодействия должны уже сказываться не только в моменты столкновений.

Начнем с того, что учтем в уравнении состояния (которое мы будем писать для одного моля газа) ограниченную сжимаемость газа. Для этого надо в уравнении идеального газа Р = RT/V

заменить объем V разностью (V-b), где b - некоторая положительная постоянная,

учитывающая размеры молекул. Уравнение

показывает, что объем не может быть сделан меньшим, чем Ь, поскольку при V -» b давление Р обращается в бесконечность.

Учтем теперь притяжение молекул. Это притяжение должно приводить к уменьшению давления газа, поскольку на каждую молекулу, находящуюся вблизи стенки сосуда, будет действовать со стороны остальных молекул сила, направленная внутрь сосуда. В грубом приближении эта сила будет пропорциональна числу молекул в единице объема, то есть концентрации газа.

С другой стороны, давление само пропорционально этому же числу. Поэтому общее уменьшение давления, связанное с взаимным

или, иначе,

Это — так называемое уравнение Ван-дер-Ваальса, или уравнение состояния реального газа, записанное для одного моля. Для произвольного

притяжением молекул, будет обратно пропорционально квадрату его объема. В соответствии с этим вычтем из (11.1) выражение

При большом разрежении газа (большие объемы V) величинами а и b можно пренебречь, и мы возвращаемся к уравнению Менделеева — Клапейрона. Ниже мы увидим, что уравнение (11.3) правильно описывает характер явлений и в обратном предельном случае больших сжатий.

Для исследования поведения реального газа, описываемого уравнением Ван-дер-Ваальса, рассмотрим определяемые этим уравнением изотермы - кривые зависимости Р от V при заданных значениях Т. С этой целью перепишем лтавнение М1.2) (лля олного моля) в виде

При заданных значениях Р и Т - это уравнение третьей степени относительно неизвестного V.

Как известно, уравнение третьей степени имеет три корня, из которых вещественными могут быть либо все три, либо один (в последнем случае уравнение имеет также два комплексно сопряженных корня). Физическим смыслом объема могут обладать, разумеется, лишь вещественные (причем положительные) корни. Поэтому заданным значениям Р и Т по уравнению Ван-дер-Ваальса соответствуют либо три различных, либо одно значение объема.

Второй случай всегда имеет место при достаточно высоких температурах.

Соответствующие изотермы мало отличаются от

45

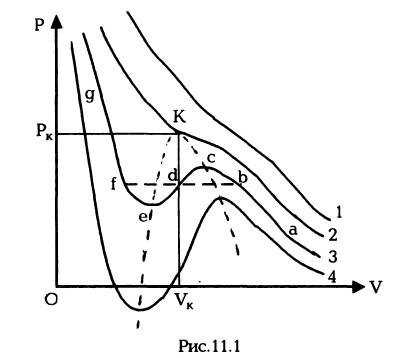
изотерм идеального газа и являются монотонно спадающими кривыми (кривая 1 на рис.11.1; увеличение номера кривых соответствует убыванию температуры). При более же низких температурах изотермы имеют максимум и минимум (кривые 3, 4_Г), так что для каждой из них существуют такие интервалы давлений, в которых кривая определяет три различных значения V (три точки пересечения изотермы с горизонтальной прямой).

Рассмотрим изотерму 3 и выясним, какой смысл имеют различные ее участки. На участках де и са зависимость давления от объема имеет нормальный характер - давление уменьшается при увеличении объема.

Участок же ее соответствовал бы неестественному положению, когда сжатие вещества приводило бы к уменьшению давления. Наличие заведомо неосуществимого участка ее изотермы означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распадение вещества на две фазы.

Другими словами, истинная изотерма будет иметь вид ломаной линии abfg. Часть ее ab отвечает газообразному состоянию вещества, а часть fg — жидкому состоянию. Горизонтальный же прямолинейный отрезок bf соответствует двухфазным состояниям — переходу газа в жидкость, происходящему (при заданной температуре) при определенном постоянном давлении. Можно показать, что отрезок bf должен быть расположен так, чтобы были одинаковы площади bed и def.

При повышении температуры прямолинейный участок изотермы уменьшается и обращается в нуль (на изотерме 2) при температуре, которая называется критической. Проходящая через эту точку изотерма 2 разделяет изотермы двух типов: монотонные изотермы вида 1 и изотермы 3, 4 с минимумами и максимумами, на которых неизбежно распадение вещества на две фазы (жидкость и газ). При критической температуре плотность пара (газа) становится равной плотности жидкости, и пар становится неотличим от жидкости.

Используя уравнение (11.4), нетрудно доказать, что

2. Первое начало термодинамики

Обратимся теперь к энергетической стороне процесса изменения состояния какого-либо тела.

Любое тело (твердое, жидкое, газообразное), находящееся в определенном состоянии, которое характеризуется его макроскопическими

параметрами Р, V и Т, обладает определенным запасом внутренней энергии U. Внутренняя энергия тела складывается из кинетической энергии поступательного движения молекул, кинетической энергии вращения молекул, кинетической энергии движения атомов внутри молекулы (если молекула не одноатомная), потенциальной энергии взаимодействия между атомами и потенциальной энергии взаимодействия молекул между собой. В нее, однако, не входит кинетическая энергия движения тела как целого и потенциальная энергия внешних сил, действующих на тело.

помощью какого процесса произошел этот переход, и

Внутренняя энергия тела является функцией его состояния. Это означает, что при переходе

начальном и конечном состояниях. Если над телом совершается циклический процесс, в результате которого тело возвращается в исходное состояние, то изменение внутренней энергии за цикл

означает, что бесконечно малое изменение внутренней энергии dU при любом процессе является полным дифференциалом.

Внутреннюю энергию тела можно изменить двумя способами:

если оно ее отдает. В этом случае изменение внутренней энергии

2) Наше тело можно теплоизолировать и

предоставить телу возможность совершить работу 6А над окружающими телами. В первом случае б А

— положительной

случае изменение внутренней энергии

Если же тело может получать (или отдавать)

1) Привести тело в контакт с более нагретым или менее нагретым телом. При этом наше тело может получать или отдавать энергию, которая

46

Это важное соотношение выражает закон сохранения энергии при тепловых процессах. Его называют первым началом термодинамики.

Для конечного процесса

Наконец, при изотермическом процессе (Т = const)

Нетрудно доказать, что при циклическом процессе работа А числено равна площади петли цикла на диаграмме Р —V и положительна, если процесс происходит по часовой стрелке (рис.11.3).

процесса, с помощью которого тело переводится из состояния 1 в состояние 2. Поэтому говорят,

процесса (а не состояния, как внутренняя энергия U). Из (11.10) следует, что при циклическом

3. Работа при изменении объема

Рассмотрим теперь каждое из слагаемых, вхоляших в пепвое начало тепмолинамики (11.9).

При изменении объема от

производит над окружающими его телами механическую работу. Если объем тела увеличивается на dV, то тело совершает бесконечно малую или элементарную работу

4. Теплоемкость

Определим теперь количество теплоты, которое необходимо сообщить телу для его нагревания или отнять от тела для его охлаждения. Конечно, это количество теплоты зависит от массы тела и от того, на сколько градусов должна быть изменена его температура. Поэтому для характеристики тепловых свойств тела пользуются особой величиной — теплоемкостью.

По определению теплоемкостью тела С называется количество тепла, которое нужно подвести или отнять у тела для изменения его температуры на 1 К.

Теплоемкость, отнесенная к единице массы

тела М называется удельной теплоемкостью

и численно равна площади (см. рис.11.2) под кривой процесса на диаграмме зависимости

Следует отметить, что формулы (11.12) и (11.13) верны для любых тел. Найдем работу, которую совершает идеальный газ при различных процессах.

Теплоемкость, отнесенная к одному молю вещества, называется молярной теплоемкостью

Обе эти теплоемкости уже характеризуют не само тело, а вещество, из которого тело состоит. Из определения теплоемкости тела следует, что

Пусть нагревание происходит при постоянном объеме (V = const). Соответствующая теплоемкость называется теплоемкостью при постоянном

47

Следовательно, подводимое к телу тепло SQ расходуется на изменение температуры dT (изменение внутренней энергии) и изменение объема dV (с этим связана механическая работа).

или на основании (11.19):

Если при нагревании постоянным остается давление, то теплоемкость называется теплоемкостью при постоянном давлении С_Р:

и показатель адиабаты

что хорошо согласуется с экспериментом.

Нетрудно показать, что выражение (11.22) можно записать через у:

Для идеального газа

следовательно,

5. Внутренняя энергия газа

Начнем с нахождения внутренней энергии идеального газа, которая, как мы знаем, состоит из кинетической энергии поступательного движения молекул газа, кинетической энергии вращения молекул и из энергии колеблющихся внутри молекулы атомов. Каждый из этих трех видов движения вносит определенный вклад и в теплоемкость газа.

Легче всего определить внутреннюю энергию одноатомного идеального газа (таковы благородные газы Не, Ne, Аг), которая представляет собой просто сумму кинетических энергий поступательного движения его частиц. Поскольку по определению температуры средняя

Попытаемся теперь найти внутреннюю энергию идеального газа, состоящего из многоатомных молекул. Как мы знаем из предыдущей лекции, на каждую из трех поступательных степеней свободы приходится кТ/2 кинетической энергии. Согласно классической механике такой результат получился бы для всех вообще степеней свободы молекулы, связанных как с поступательным движением, так и с ее вращением и с колебаниями атомов в ней.

Действительно, в классической (в отличие от квантовой) физике доказывается так называемая теорема о равномерном распределении кинетической энергии по всем степеням свободы молекул. Эту теорему можно сформулировать так: если система молекул находится в состоянии теплового равновесия при температуре Т, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы молекулы и для каждой степени свободы молекулы она равна кТ/2.

Мы знаем также, что при колебательном движении (см. лекцию 5) среднее значение потенциальной энергии равно среднему значению кинетической энергии, поэтому можно сделать вывод, что на одну колебательную степень свободы приходится энергия кТ (кТ/2

кинетической и кТ/2 потенциальной). В дальнейшем мы будем считать, что на колебательную (как на поступательную и вращательную) степень свободы приходится энергия кТ/2, но число колебательных степеней

будем удваивать.

Если обозначить полное число степеней свободы молекулы буквой i (с удвоенным количеством колебательных степеней), то внутренняя энергия газа из N таких молекул

то внутренняя энергия газа, состоящего из N одноатомных молекул

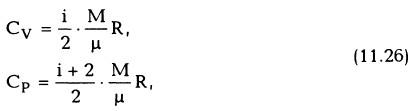
Поэтому его теплоемкости (на основании (11.17) и (11.21))

Его теплоемкости

48

Выражение для внутренней энергии (11.24) через у остается в силе.

В качестве примера рассмотрим газ, состоящий из двухатомных молекул. Полное число степеней свободы такой молекулы равно шести (шесть координат двух атомов). Поступательных степеней — три (три координаты центра масс молекулы), вращательных — две (вращение молекулы вокруг двух взаимно перпендикулярных осей, проходящих через центр масс и лежащих в плоскости, ортогональной оси молекулы). Остается одна колебательная степень свободы. Согласно (11.28)

сказывается на теплоемкости газа лишь при достаточно высоких температурах. При обычных температурах колебательные степени свободы как бы "заморожены" и не дают вклада в теплоемкость. В области комнатных температур теплоемкости двухатомных газов связаны лишь с поступательным и вращательными движениями молекул и очень близки к своим теоретическим значениям (i = 5)~

Найдем теперь внутреннюю энергию реального газа, подчиняющегося уравнению Ван-дер-Ваальса. Она включает в себя дополнительно к энергии идеального газа потенциальную энергию взаимодействия молекул между собой. Можно доказать, что внутренняя энергия моля реального газа

что не согласуется с опытом при обычных температурах.

Дело в том, что, как показывает квантовая теория, колебательное движение атомов

где а - постоянная, входящая в уравнение Ван-дер-Ваальса.

49

Лекция 12. ПРЕОБРАЗОВАНИЕ ТЕПЛОТЫ В РАБОТУ

Адиабатический процесс; необратимость тепловых процессов; преобразование теплоты в механическую работу; цикл Карно; энтропия; второе начало термодинамики, сформулированное с помощью энтропии; физический смысл энтропии.

1. Адиабатический процесс

Займемся теперь изучением некоторых простейших тепловых процессов (кроме изохорического, изобарического и

изотермического).

Очень простым процессом является расширение газа в пустоту: газ вначале находится в части сосуда, отделенной от другой части перегородкой, а после открывания отверстия в перегородке заполняет весь сосуд. Так как при таком расширении газ не совершает никакой работы, то его энергия U остается постоянной. У идеального газа энергия зависит, как мы уже знаем, только от температуры; поэтому из постоянства энергии следует также и постоянство температуры идеального газа при его расширении в пустоту. Температура же реальных газов при расширении в пустоту изменяется.

Очень сильно отличается от расширения в пустоту другой процесс расширения газа, называемый адиабатическим.

Для адиабатического процесса характерно, что газ все время остается под внешним давлением, равным давлению самого газа. Другое условие адиабатичности состоит в том, что в течение всего процесса газ остается теплоизолированным от внешней среды, т.е. никуда не отдает и ниоткуда не получает тепла.

Наиболее просто представить себе адиабатическое расширение (или сжатие) газа, находящегося в теплоизолированном

цилиндрическом сосуде, снабженном поршнем. Для выполнения первого условия адиабатичности поршень должен двигаться достаточно медленно, чтобы газ, следующий за поршнем, успевал перейти в состояние теплового равновесия, ₍ соответствующего мгновенному положению поршня.

При слишком быстром вдвигании поршня газ не успевал бы следовать за ним и под поршнем возникала бы область пониженного давления, в которую бы и расширялся остальной газ; такой процесс не был бы адиабатическим. Анализ показывает, что условие адиабатичности выполняется, если скорость поршня мала по сравнению со скоростью звука в газе.

Для выполнения второго условия требуется, с другой стороны, достаточная быстрота процесса, так как за время его протекания газ не должен успеть обменяться теплом с окружающей средой.

При адиабатическом процессе уже нельзя утверждать, что остается постоянной внутренняя энергия газа, поскольку газ при расширении совершает работу (или, при сжатии, над ним совершается работа). Общее уравнение

адиабатического процесса мы получим, если в первом начале термодинамики положим

в соответствии с условием теплоизолированности. Таким образом, при адиабатическом процессе

откуда

Выражение (12.3) показывает, что газ совершает работу за счет убыли своей внутренней энергии.

Вспомнив, что для идеального газа

Применим теперь уравнение (12.2) к

Интегрируя (12.5), получим после несложных преобразований, что при адиабатическом процессе

расширение сопровождается охлаждением, а сжатие — нагреванием газа.

Комбинируя уравнение (12.6) с формулой

соотношение, связывающее изменение

температуры и давления при адиабатическом процессе

50

связывающее давление и объем (последнее равенство называют уравнением адиабаты Пуассона).

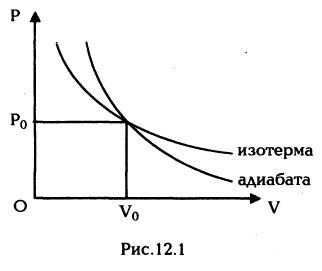
При изотермическом расширении газа его