
- •Производная
- •1.1. Определение производной
- •Правила дифференцирования
- •1.2. Дифференцирование неявных функций
- •1.3. Логарифмическое дифференцирование
- •1.4. Производные высших порядков
- •1.5. Дифференцирование функции, заданной параметрически
- •1.6. Уравнение касательной к нормали
- •2. Исследование поведения функций
- •2.1. Возрастание и убывание функции
- •2.2. Максимум и минимум функций
- •2.3. Выпуклость и вогнутость кривой. Точки перегиба
- •2.4. Асимптоты
- •3. Наибольшее и наименьшее значения функции на отрезке
- •4. Правило лопиталя
- •Задания к контрольной работе № 2
- •Первообразная и неопределенный интеграл
- •Свойства интегралов
- •Методы интегрирования
- •1. Непосредственное интегрирование
- •2. Метод замены переменной (подстановки)
- •3. Метод интегрирования по частям
- •Интегрирование рациональных дробей
- •1. Простейшие дроби, их интегрирование к простейшим дробям относятся дроби вида:
- •2. Правильные и неправильные рациональные дроби
- •3. Разложение правильной дроби
- •4. Нахождение коэффициентов
- •5. Правило интегрирования рациональных дробей
- •Интегрирование некоторых иррациональностей
- •Интегрирование тригонометрических выражений
- •Определенный и несобственный интегралы, их вычисление
- •Геометрические приложения определенного интеграла
- •Задачи к контрольной работе № 3
Департамент образования г. Москвы
Государственное образовательное учреждение среднего профессионального образования
Московский государственный техникум технологии, экономики и права им. Л. Б. Красина
|
|
УТВЕРЖДАЮ |
|
|
Зам директора по учебной работе |
|
|
______________/Вовк Н. И./ «____»_________________20___г. |
Методические указания и задания для контрольных работ
по дисциплине
Математика
для студентов заочного отделения
специальностей
030912
Право и организация социального обеспечения
(базовый уровень)
-
Производная
1.1. Определение производной
Пусть
на множестве
 задана функция
задана функция
 .
Фиксируем точку
.
Фиксируем точку
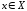 и задаем приращение аргумента
и задаем приращение аргумента
 .
Тогда точка
.
Тогда точка
 соответствует
соответствует
 и
и
 называется приращением функции.
называется приращением функции.
Если существует предел
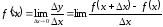 ,
,
то
он называется производной функции
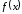 в точке
в точке
 .
.
Существуют
и другие обозначения производной:
 ,
,
 .
.
Операция
вычисления производной функции называется
операцией дифференцирования, а если
 конечна, то функция
конечна, то функция
 называется дифференцируемой.
называется дифференцируемой.
Прежде чем воспользоваться таблицами производных, надо установить, является функция простой или сложной.
Функция
 называется сложной, если
называется сложной, если
 есть функция от
есть функция от
 :
:
 ,
т. е.
,
т. е.
 .
.
Производная сложной функции вычисляется по формуле
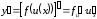 ,
,
т.
е. сначала вычисляется производная
функции
 по переменной
по переменной
 ,
и затем она умножается на производную
функции
,
и затем она умножается на производную
функции
 по переменной
по переменной
 .
.
Правила дифференцирования
-
 (
( – const)
– const) -
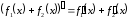
-

3а.

-
 (
( )
) -
 ,
если
,
если
 ,
,
 .
.
Разумеется,
что для справедливости этих правил
необходимо существование производных
 ,
,
 ,
,
 ,
,
 .
.
Таблица производных
1.
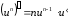 (
( ) 2.
) 2.

3.
 4.
4.

5.
 6.
6.
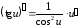
7.
 8.
8.
 (
( )
)
9.
 (
( ) 10.
) 10.

11.
 12.
12.
 (
( )
)
13.
 14.
14.

15.

Пример 1. Найти производные функций:
а)
 ; б)
; б)
 ; в)
; в)
 .
.
Решение.
а) Функция
 – это произведение двух функций
– это произведение двух функций
 и
и
 ,
поэтому по третьему правилу
дифференцирования:
,
поэтому по третьему правилу
дифференцирования:
 .
.
Из
таблицы производных находим, что
 ,
и так как
,
и так как
 ,
то
,
то
 ;
;
 .
.
Значит,
 .
.
б)

 .
.
в)

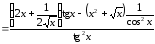 .
.
Пример 2. Найти производные функций:
а)
 ; б)
; б)
 ; в)
; в)
 .
.
Решение.
а) Функция
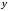 – это сложная функция
– это сложная функция
 ,
,
 .
Тогда по формуле 1 таблицы производных
.
Тогда по формуле 1 таблицы производных
 ,
а по формуле 5
,
а по формуле 5
 .Таким
образом,
.Таким
образом,
 .
.
б)
Используем правило дифференцирования
3а:
 .
Функция
.
Функция
 – сложная
– сложная
 ,
,
 .
Поэтому
.
Поэтому
 .
.
в)



 .
.
1.2. Дифференцирование неявных функций
Если
функция
 такова, что подстановке ее в уравнение
такова, что подстановке ее в уравнение
 ,
последнее обращается в тождество, то
говорят о неявном задании функции
,
последнее обращается в тождество, то
говорят о неявном задании функции
 .
Например, уравнение
.
Например, уравнение
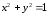 неявно задает функцию
неявно задает функцию
 (а также функцию
(а также функцию
 ).
Однако не всегда удается перейти от
неявного задания функции к явному.
).
Однако не всегда удается перейти от
неявного задания функции к явному.
Пусть
дифференцируемая функция
 задана уравнением
задана уравнением
 .
Тогда дифференцируем левую и правую
часть уравнения, считая
.
Тогда дифференцируем левую и правую
часть уравнения, считая
 сложной функцией, и выражаем из уравнения
сложной функцией, и выражаем из уравнения
 .
.
Пример
3. Найти
производную функции
 .
.
Решение.
 ;
;
 .
.
Так
как
 ,
,
 ,
,
 ,
,
 ,
,
то
 .
.
Слагаемые,
содержащие
 ,
переносим в левую часть, а все остальное
в правую:
,
переносим в левую часть, а все остальное
в правую:
 ,
,
 .
.
1.3. Логарифмическое дифференцирование
Довольно
часто возникает необходимость вычисления
производной сложной функции
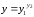 ,
где
,
где
 ,
,
 – дифференцируемые функции. В этом
случае поступим следующим образом:
логарифмируем
– дифференцируемые функции. В этом
случае поступим следующим образом:
логарифмируем
 –
–
 ,
,
продифференцируем
это равенство по
 –
–
 ,
,
 .
.
Отсюда имеем:
 .
.
Нет необходимости запоминать эту формулу. Достаточно понять идею – функцию сначала логарифмируем, затем дифференцируем полученное равенство и находим производную.
Пример
4. Найти
производную функции
 .
.
Решение.
Логарифмируем функцию
 :
:
 .
.
Дифференцируем
это равенство по
 :
:


 .
.
Поэтому
 .
.
1.4. Производные высших порядков
Если
производная
 функции
функции
 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
 и имеет в этой точке производную, то эта
производная от
и имеет в этой точке производную, то эта
производная от
 называется второй производной (или
производной второго порядка) функции
называется второй производной (или
производной второго порядка) функции
 в точке
в точке
 и обозначается одним из следующих
символов:
и обозначается одним из следующих
символов:
 ,
,  ,
, 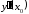 ,
,  ,
,  ,
, 
 .
.
Третья
производная определяется как производная
от второй производной и т. д. Если уже
введено понятие
 -й
производной и если
-й
производной и если
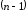 -я
производная имеет производную в точке
-я
производная имеет производную в точке
 ,
то указанная производная называется
,
то указанная производная называется
 -й
производной (или производной
-й
производной (или производной
 -го
порядка) и обозначается
-го
порядка) и обозначается
 ,
,
 или
или
 ,
,
 .
.
Таким образом, производные высших порядков определяются индуктивно по формуле:
 .
.
Функция,
имеющая
 -ю
производную в точке
-ю
производную в точке
 ,
называется
,
называется
 раз дифференцируемой в этой точке.
раз дифференцируемой в этой точке.
Пример
5. Найти
 функции
функции
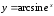 .
.
Решение.


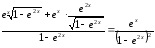 .
.
Пример
6. Найти
 ,
если
,
если
 .
.
Решение.
Находим
 .
.
 .
.
Теперь
найдем вторую производную
 .
Имеем
.
Имеем

 .
.
