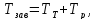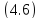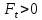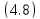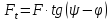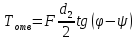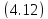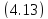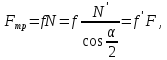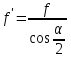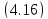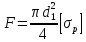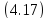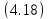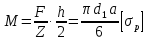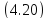4.2 Соотношение сил и моментов в резьбовых деталях при затяжке

При завинчивании гайки или винта (рис. 4.5) к ключу прикладывают момент завинчивания:

где – момент сил трения на торце гайки, – момент сил трения в резьбе.

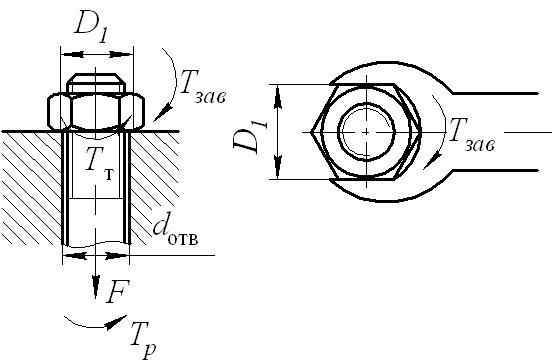
Рис. 4. 5

Приведенный радиус сил трения на торце гайки принимаем

Тогда

где – коэффициент трения на торце гайки.

Момент сил трения в резьбе определяем, рассматривая гайку как ползун, поднимающийся по виткам резьбы (рис. 4.6).

Рис. 4. 6

Согласно теореме механики ползун находится в равновесии, если равнодействующая 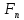внешних сил отклонена от нормали n-n на угол трения φ. Внешними силами являются: осевая сила F и окружная сила . Из рис. 4.6 следует

где ψ – угол подъема резьбы; – угол трения в резьбе.

Тогда момент завинчивания:

Рассмотрим момент отвинчивания гайки 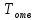(рис. 4.7).

Рис. 4. 7

При этом окружная сила 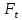и силы трения меняют свое направление. Принимаем направление и при завинчивании положительным. Тогда 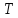и при отвинчивании должны быть отрицательными. Таким образом, чтобы отвинчивания не происходило, должны выполняться условия:

Условие самоторможения можно записать в виде без учета :

Рассмотренные уравнения составлены для прямоугольной резьбы. При треугольной резьбе коэффициент трения изменится.

Связь между коэффициентом трения в прямоугольной и треугольной резьбах легко получить, если предположить, что витки резьбы перпендикулярны оси винта (рис. 4.8).

Рис. 4. 8

Силы трения в прямоугольной и треугольной резьбах определятся выражениями (4.13) и (4.14) соответственно:

где 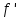- приведенный коэффициент трения:

Для метрической резьбы () ; .

Для крепежных резьб , а φ изменяется от 6⁰ (при ) до 16⁰ (при ). Таким образом, все крепежные резьбы самотормозящие. Ходовые резьбы выполняют как самотормозящими, так и не самотормозящими.

Приведенные выше коэффициенты трения справедливы при статических условиях. Если нагрузки переменные, то 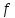снижается и происходит самоотвинчивание.

КПД винтовой пары представляет интерес главным образом для винтовых механизмов. Его можно вычислить по отношению работы, затраченной на завинчивание гайки без учета трения, к той же работе с учетом силы трения. Работа завинчивания – это произведение момента на угол поворота. Так как углы поворота равны в том и другом случаях, то отношение работ равно отношению моментов:

где определяется по формуле (4.7), а 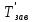- по той же формуле, но при .

4.3 Расчет резьбы на прочность

В винтовой паре силы 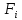, нагружающие витки резьбы, не равны между собой (рис. 4.9).

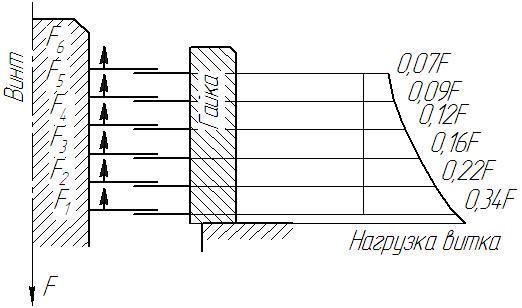
Рис. 4. 9

График распределения нагрузки по виткам свидетельствует о значительной перегрузке нижних витков и нецелесообразности увеличения витков гайки, так как верхние витки мало нагружены.

Теоретические и экспериментальные исследования позволили разработать конструкции специальных гаек, выравнивающие распределение нагрузки в резьбе (рис. 4.10).

Рис. 4. 10

В наиболее нагруженной нижней зоне висячая гайка тоньше и обладает повышенной податливостью, что способствует выравниванию нагрузки в резьбе.

При расчете на прочность полагаем, что нагрузка распределяется по виткам равномерно, и усилие, воспринимаемое каждым витков, по всей поверхности также распределяется равномерно.

Причинами выхода из строя резьбы являются (рис. 4.11): разрыв стержня винта по внутреннему диаметру (4.17), смятие по поверхности витка (4.18), срез по кольцевой поверхности АС (4.19), изгиб витка (4.20, рис. 4.12).

Рис. 4. 11

где - число витков. Площадь смятия представляет собой проекцию поверхности витка на плоскость, перпендикулярную оси витка.

Рис. 4. 12

ГОСТ предусматривает такие размеры резьбы, при которых все виды разрушения равновероятны (принцип равнопрочности). Это условие требует равенства предельных нагрузок при всех видах разрушения.

Стандартные высоты гаек и глубины завинчивания исключают необходимость расчета резьбы по всем четырем видам разрушения, при этом достаточно выполнения только расчета стержня на разрыв (4.17).

В соответствии с принципом равнопрочности высоту нормальных стандартных гаек крепежных изделий принимают: